trójkąty wpisane i opisane na okręgu kurdefix: udowodnij, że w trójkącie abc symetralna boku bc przecina dwusieczną kąta bac w punkcie d leżącym na okręgu opisanym na trójkącie abc.

Basia: hmm..................... a jeżeli trójkąt BAC będzie równoramienny i BA=AC ? wtedy symetralna BC i dwusieczna ∡BAC są tą samą prostą jeżeli proste się pokrywają to się nie przecinają po wykluczeniu tego przypadku wydaje się to być prawdą, ale nie mam pomysłu na dowód

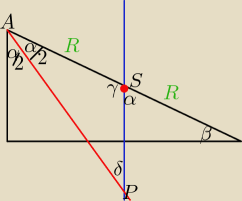
Basia: w trójkącie prostokątnym łatwo to udowodnić dowód: β=90−α γ=180−α

	α		α		α
δ = 180−γ−		= 180 − (180−α) −		=		⇒
	2		2		2

△ASP jest równoramienny ⇒ SP = SA = R ⇒ P∊o(S,R) może da się to jakoś uogólnić

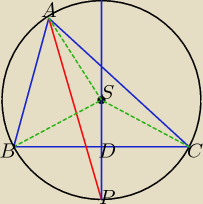
Basia: ∡BSC = 2α ∡BSD = α ⇒ ∡DBS = 90−α ∡SBA = ∡SAB = β−90+α

	180−2γ
∡SBA = ∡SAB =		= 90 − γ
	2

	α		α
∡SAP = ∡SAB −		= 90−γ−
	2		2

∡ASP = ∡ASB + ∡BSD = 2γ+α

	α		α
∡SPA = 180 − ∡ASP − ∡SAP = 180 − 2γ −α − 90+γ+		= 90−γ−
	2		2

∡SAP = ∡SPA ⇒ SA = SP = R ⇒ P∊o(S,R) proszę to sprawdzić, bo mi się już te kąty w oczach mienią i niczego nie jestem pewna

Basia: P.S. trzecia linijka od góry jest niepotrzebna P.S.2 zmień sobie nick

kurdefix: a dlaczego ∡BSD=α ? przecież to symetralna a nie dwusieczna