viola7244: Witam czy ktoś by mi pomógł to zrobić bo
jakaś tempa jestem z tego działu a)Znajdź współrzędne obrazów punktu A=(3,−1) w symetrii
względem punktu (0,0) i w symetrii względem osi y b)Znajdź współrzędne obrazów punktu B=(4,2)
w symetrii względem punktu (1,3) i w symetrii względem prostej o równaniu x=1
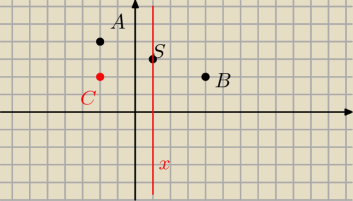a) że punkt to (0,0) zmieniasz współrzędne na przeciwne, czyli A'=(−3,1).
Koniecznie narysuj to sobie w układzie. (W geometrii analitycznej niemal nie da się zrobić
błędu, bo wszystko można sprawdzić na rysunku)
b)
A− obraz B(4,2) względem S(1,3)
BS=SA − wektory
[1−4,3−2]=[x−1,y−3]
[−3,1]=[x−1,y−3]
−3=x−1 i y−3=1
x=−2 y=4
A(−2,4)
c)
C− obraz B względem x=1
prosta przechodząca przez punkt B i prostopadła do x=1 to y=2, czyli C=(x,2)
1249→ tu masz wzór na odległość punktu od prostej
x−1=0
| |4*1+2*0−1| | ||
d= | =|3|=3− odległość B od x | |
| √1+0 |
| |x*1+2*0−1| | ||
d'= | =|x−1| | |
| √1+0 |
