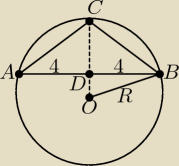
Oblicz promień okręgu. Planimetria Agniesia: Trójkąt ABC jest trójkątem równoramiennym. Punkt O jest środkiem okręgu opisanego na tym trójkącie. Oblicz promień tego okręgu. IDCI = 3

Agniesia: Nie wiem jak sie do tego zabrać

Nienor: ICBI=5 (z Pitagorasa)

	1		8*5*5
PΔABC=		*3*8=
	2		4R

Agniesia: a jak ten promień obliczyć

Mila: Korzystając z wpisu Nienor

	50
12=		/*R
	R

12R=50

	50
R=
	12

	25
R=
	6

olo: jak to obliczyc ?

Mila: Czego nie wiesz?

Eta: P=12 , |CB|=|AC|=5 , |AB|=8

	5*5*8
R=		=.......
	4P

+-: CB j/w Z podobieństwa trójkątów

3		2,5
	=		R={12,5}{3}={25}{6}
5		R

pigor: ... lub z ΔBDO i tw. Pitagorasa: (R−3)²+4²=R² ⇔ ⇔ R²−6R+9+16=R² ⇔ 25=6R ⇔ R=²⁵₆ ⇔ R=4¹₆. ...

Marcin: Dlaczego jest tu wzór a*b*c/4R?

Janek191:

	a*b*c
P =
	4 R

Wzór na pole dowolnego Δ wpisanego w okrąg o promieniu długości R.

Marcin?: a skąd się wziął wzór na te duże R, co napisała Eta?