Okręgi i inne figury Ania534: Pmocy Środek okręgu opisanego na trapezie równoramiennym należy do tego trapezu. Jedna z podstaw dzieli ten okrąg na łuki, których długości są w stosunku 4:5, a druga dzieli okrąg na łuki w stosunku 2:7. Wyznacz kąty trapezu.

Basia:

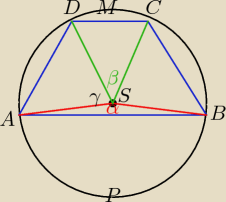
łukAPB		4		α		4		4
	=		⇒		=		⇒ α =		*360 = 4*72 = 288
2πR		5		360		5		5

łukDMC		2		β		2		2		720
	=		⇒		=		⇒ β =		*360 =
2πR		7		360		7		7		7

trapez jest równoramienny (bo tylko na takim można opisać okrąg) ⇒ ∡ASD = ∡BSC = γ

	720
2γ+288+		= 360
	7

wylicz γ i skorzystaj z tego, że trójkąty: ASD; ASB i CSD są równoramienne

Basia: źle przeczytałam treść

łukAPB		4		4		α		4		4
	=		=		⇒		=		⇒ α=		*360 = 160
2πR		4+5		9		360		9		9

łukDMC		2		2		β		2		2
	=		=		⇒		=		⇒ β=		*360 = 80
2πR		2+7		9		360		9		9

trapez jest równoramienny (bo tylko na takim można opisać okrąg) ⇒ ∡ASD = ∡BSC = γ 2γ+160+80 = 360 wylicz γ i skorzystaj z tego, że trójkąty: ASD; ASB i CSD są równoramienne