napisz równanie prostej, gdy a jest liczbą całkowitą.
Fiedor.: Prosta l przechodzi przez punkt D=(−3,2) i przecina osie układu współrzędnych w takich punktach
A i B ze |AB|= 4* p(5). Napisz równanie prostej l, gdy współczynnik kierunkowy jest liczba
całkowitą.
Oznaczyłem A=(m,0) i B=(0,b) sz: l: y=ax+b, a należy do C.
D należy do pr. l => 2=−3a+b
b=2+3a => l: y=ax + 2 + 3a oraz B=(0, 2+3a) bo b to wyraz wolny
prostej l, czyli pkt. przecięcia się prostej z osią OY. nie wiem co dalej, proszę o pomoc
21 wrz 19:58
Eta:
To może tak: A( x
A, 0) B( 0,y
B)
AB: y= ax+b
| | −b | |
A( |
| , 0) , B(0,b) i a€C |
| | a | |
| | −3a−2 | | 2 | |
yB=b= 3a+2 to: xA= |
| = −3− |
| więc a musi być dzielnikiem 2 |
| | a | | a | |
czyli a={1, −1, 2, −2}
dla a= 1 x
A= −5 i y
B= 5
a= −1 x
A= −2 i y
B= −1
a= 2 x
A= −4 i y
B= 8
a= −2 x
A= −2 i y
B= −4
teraz należy sprawdzić dla których punktów A i B długość |AB|= 4
√5
|AB|
2= (
√5)
2= 80
tylko dla x
A= −4 i y
B= 8 bo (−4)
2+8
2= 80
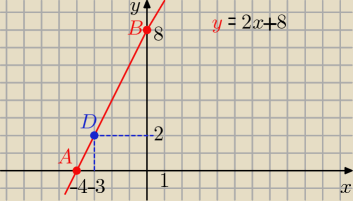
zatem A(−4,0), B(0,8)
to AB: y= ax+b ⇒ AB: .......... dokończ
21 wrz 20:42
Mila:
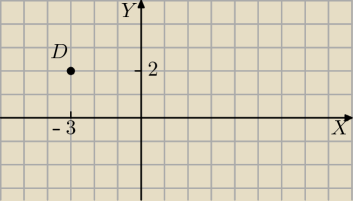
D=(−3,2)
y=ax+b
2=−3a+b
b=2+3a
y=ax+2+3a
A=(m;0) m − miejsce zerowe
a*m+2+3a=0
B=(0;2+3a)
AB=
√m2+(2+3a)2
Czy tam jest AB=4
√5?
21 wrz 20:47
Eta:
21 wrz 20:52
Fiedor.: tak, przepraszam. 4
√5 oczywiście. Mila, robiłem podobnie jak Ty, ale rozwiązanie tego
równania zajęło mi stronę A5, a potem jeszcze wyliczanie m, podstawianie do wzoru na prostą,
to pewnie 3x tyle. to musi się dać prościej zrobić
@Eta, dziękuję
21 wrz 20:56
Fiedor.: odpowiedź się zgadza, z tym co jest z tyłu. Jeszcze raz dziękuję
21 wrz 20:57
Eta:
21 wrz 21:02
Mila: Równanie nieciekawe, ale ma jedno rozwiązanie całkowite a=2 i mamy równanie prostej .
m nie trzeba liczyc.
Nurtuje mnie sposób mniej pracochłonny. ( oprócz odgadnięcia)
21 wrz 21:59
Eta:
Sposób podany przeze mnie nie jest aż tak pracochłonny
21 wrz 23:44
Mila: Myślisz o sposobie z 20:42?
21 wrz 23:46
Mila: Poza tym oceniałam swój sposób.
21 wrz 23:47
Mila: kontynuując moje rozwiązanie :
po rozwinięciu i uporządkowaniu, korzystając z tw Bezou'ta ustaliłam, że a=2.
II sposób, mniej czasochłonny:
| | 2+3a | |
(*) ( |
| )2+(2+3a)2=80 |
| | a | |
a∊C z założenia, to (2+3a)∊C ⇒ (2+3a)
2∊C⇒
| | 2+3a | |
( |
| )2∊C, aby otrzymać wynik sumy całkowity |
| | a | |
{2+3a}{a})∊C⇔(U{2}{a)+3) ∊C⇔a∊{1,−1, 2,−2}
sprawdzamy dla jakiego a spełnione jest równanie(*)
a=2
to b=8
y=2x+8
22 wrz 17:36
Mila: Poprawa zapisu
| | 2+3a | | 2 | |
( |
| )∊C⇔( |
| +3) ∊C⇔a∊{1,−1, 2,−2} |
| | a | | a | |
22 wrz 22:35