prosze o pomoc zos: W trójkącie ABC, |AB|=15cm, poprowadzono odcinek DE równoległy do boku AB. Pole trójkąta DEC jest równe 12cm2, a pole trapezu ABED 13cm2. Oblicz: a)długość odcinka DE b)|CE|EB|

pigor: ... np. tak : z podobieństwa ΔDEC ∼ ΔABC (cecha kkk) , tw. o stosunku pól powierzchni ΔΔ podobnych i warunków zadania :

	|DE|		12		|DE|		12		4
a) k2= (		)2=		⇒ k=		= √		=		√3 ⇒
	15		12+13		15		25		5

k= ⁴₅√3 = 0,8√3 − skala podobieństwa i |DE|= 12√3 cm ; −−−−−−−−−−−−−−−−−−−−−−−−−−−− b) z podobieństwa tych ΔΔ lub z tw. Talesa : . ...

Skipper:

	10
25=15H/2 50=15H H=
	3

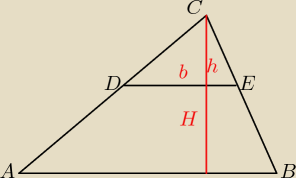
12=bh/2 24=bh b=24/h

	15+b		10		15+24/h	10−3h
13=		(		−h) 13=
	2		3		2	3

	24
78=(15+		)(10−3h)
	h

78=150−45h+240/h−72 78h−150h+45h²−240+72h=0 45h²=240

	48		4√3
h2=		h=
	9		3

znając {H}{h} ... policzymy resztę (mam nadzieję, że nie popaprałem w liczeniu)

ewa: a) tak jak napisał pigor tylko pomylił się przy obliczaniu skali:

	12		12		2√3
k2=		⇒ k=√		=
	25		25		5

	2√3
czyli |DE|=k*|AB|=		*15=6√3
	5

pigor: ... no tak, dzięki za czujność , przepraszam i pozdrawiam . ... :0