Całki Tiamat: Oblicz pole obszaru ograniczonego liniami: y=lctgxl i y=1 (uwzględnij tylko kąty większe od 0 i mniejsze od π) Mam problem z "granicami", jedną znalazłam: ^π₄, ale drugą nie wiem jak znaleść...

Artur_z_miasta_Neptuna: |ctgx| = 1 ⇔ ctgx = 1 ⋁ ctgx = −1

	π
jako że funkcja ctg x jest nieparzysta WZGLĘDEM PROSTEJ x=		... to z faktu, że ctg
	2

	π
		= 1 wnioskujesz że dla jakiego kąta ctgx = −1
	4

Tiamat: Hmm, cóż myślę, że ³₄ π ale nie zgadza mi się to z odpowiedziami jak to liczę

Artur_z_miasta_Neptuna: to może źle liczysz

Tiamat: Może...

	sinx		dt
∫ 1− ctgx dx = ∫1dx − ∫		dx = x − ∫		= x − ln(cosx)
	cosx		t

[ x − ln(cosx)] − no i teraz używam granic [³₄π + ln(cos³₄π)] − [^π₄ + ln(cos^π₄)] Dobrze?

Tiamat:

	√2
W zasadzie prawie mi wyszło, jednak 2ln		trochę przeszkadza i nie wiem jak to skrócić
	2

w ogóle...

π		√2
	− 2ln
2		2

loitzl9006: nie no źle jest:

	cos x
ctg x =		pomyliło Ci się z tangensem...
	sin x

Tiamat: teraz to już w ogóle dziwne rzeczy mi wyszły...

3π		√2		π		√2
	+ ln		−		− ln
4		2		4		2

ln się skrócą i zostaje mi

3π		π		2π		π
	−		=		=
4		4		4		2

a odpowiedź jest inna, już nie mam pojęcia co mogłam spsuć

Artur_z_miasta_Neptuna: przecież tam masz |ctgx| więc jak chcesz to policzyć to musisz podzielić na dwie całki (od 0 do π/2 i od π/2 do π)

Tiamat: No dobra to chyba nie mój poziom, bo nie mam pojęcia jak to zrobić. W zasadzie to dlaczego tak? y=lctgxl ma tam asymptoty przecież, ale to nie są te granice chyba? Wszystko mi się pomieszało... Dramat

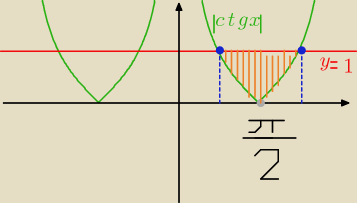
loitzl9006: Wykres funkcji |ctg x| powstaje z wykresu funkcji ctg x poprzez odbicie symetryczne względem osi x tego wszystkiego co znajduje się pod osią x w wykresie funkcji ctg x.

	π		3π
Trzeba Popatrzeć na rysunek: z niego widać że granice to x=		i x=		. Ale widać też,
	4		4

że obszar zaznaczony na pomarańczowo (liczymy pole tego właśnie obszaru) można podzielić na dwa obszary o równym polu.

	π		π
Proponuję policzyć całkę w granicach od		do		(będzie łatwo ją policzyć) ,a wynik
	4		2

potem pomnożyć przez 2. Całka do policzenia to ∫ 1 − ctgx dx

	π		π
oczywiście w granicach		do
	4		2

loitzl9006: wiesz o co mi chodzi?

Tiamat: Hmmm, czyli to co ja liczyłam było po prostu niepełne! No dobrze, licze tą całkę, ale to dalej nie jest to, ale może po pomnożeniu razy 2 coś w końcu wyjdzie:

π		√2
	− ln		l razy 2
4		2

π		√2
	− 2ln
2		2

jak skrócić ten ln?

loitzl9006: nie skracasz, jak zostawiasz w takiej postaci z ln. ale zacznijmy od tego że masz zły wynik tej całki; powinno wyjść

π		ln 2
	−
4		2

co po pomnożeniu przez 2 ma dać

π
	− ln 2 i taki ma wyjść wynik. (szukane pole całego pomarańczowego obszaru)
2

Przedstaw obliczenia całki ∫ 1 − ctgx dx, znajdziemy błąd.

Tiamat: ∫1 dx − ∫ctgx dx =

	cosx
x − ∫		dx = t=sinx dt=cosxdx
	sinx

	dt
x − ∫		=
	t

x − ln[t] = x − ln[sinx] = koniec

loitzl9006: jest ok. Wstawiamy teraz granice:

	√2
π/2 − ln[sin(π/2)] − π/4 + ln[sin(π/4)] = π/2 − ln(1) − π/4 + ln(		) =
	2

	√2		21/2
= π/4 + ln(		) = π/4 + ln(		) =
	2		21

	ln 2
= π/4 + ln(2−1/2) = π/4 −
	2

	ln 2
Możesz nie doprowadzać na siłę wyniku do postaci π/4 −		, tylko zostawić w postaci
	2

	√2
π/4 + ln(		)
	2

i pomnożyć go przez 2 − też będzie ok.

Tiamat: Odpowiedź do tego zadania wygląda tak:

π
	+ ln12
2

Czy możliwe, że gdzieś jest bład lub to po rpostu co nam wyszło jest nieskrócone? Zgadza się wszystko?;3

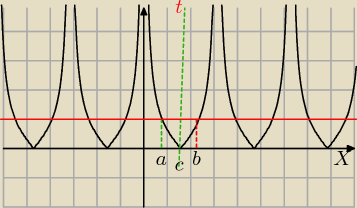
Mila: ctgx=1

	π
x=		=a
	4

ctgx=0

	π
x=		=c
	2

P=2_a∫^c(1−ctgx)dx=2*[x−ln|sinx|]_a^c=

	π		π		π		π
=2*(		−lnsin		−		+lnsin		)=
	2		2		4		4

	π		√2		π
=2*(		+ln		)=2*(		+ln√2−ln2)=
	4		2		4

	π		1
=2*(		+		ln2−ln2)=
	4		2

	π		1
=2*(		−		ln2)=
	4		2

	π		π		1
=2*(		+ln2−1)=		+ln
	4		2		2

Liczyłam, bo sugerowałeś błąd. Masz dobrze, ale w innej postaci.