proszę o sprawdzenie ARECZEEEEEEEEEEEE: wyznaczyć dziedzinę naturalną funkcji− f(x)=arcctg log(4x−5) 4x−5>0 f(x)=log arcsin2x arcsin2x>0 2x≥−1 2x≤1 no i jak policzyć arcsin2x

Artur_z_miasta_Neptuna: jaka jest dziedzina arctgx x∊(−π/2 ; π/2) więc logarytm może tylko takie wartości przyjmować

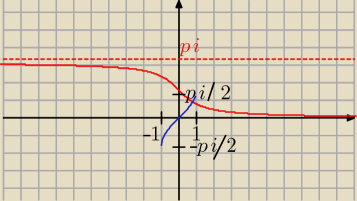Gustlik: Legenda: y=arcctgx y=arcsinx Arturze, − źle. Dziedziną arcsinx jest zbiór <−1, 1>, a dziedziną arcctgx jest R. f(x)=arcctg log(4x−5) D: 4x−5>0 (dziedzina logarytmu)

	5
x>
	4

	5
D: x∊(		, +∞)
	4

f(x)=log arcsin2x D: −1≤2x≤1 /:2 (dziedzina arcsinx)

	1		1
x∊<−		,		>
	2		2

arcsin2x>0 (dziedzina logarytmu)

	1
x∊(0,		>
	2

	1
Odp: x∊(0,		>
	2