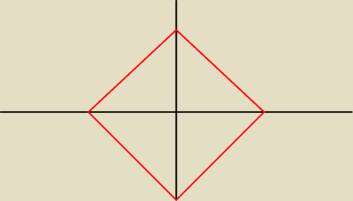
wartość bezwzględna piotr: Ile różnych rozwiązań w liczbach całkowitych ma równanie |x| + |y| ≤ 1000? czy wykonałem poprawnie rysunek?

Artur_z_miasta_Neptuna: prawie −−− jako że jest to ≤ to musisz 'zakreskować' wnętrze

piotr: no tak. ale mi wychodzi tylko 2001 a w odp jest 2001997

piotr:

Artur_z_miasta_Neptuna: bo zapewne zrobiłeś tak: x=0 i y= 1000 lub −1000 −−−− 2 rozwiązania x=1 lub x=−1 i y=999 lub y=−999 −−−−− 4 rozwiązania itd. a tam jet ≤ a nie =

Artur_z_miasta_Neptuna: dla x=0 masz 2'001 rozwiązań dla x=1 masz 1'999 rozwiązań dla x=2 masz 1'997 rozwiązań ......... dla x = n masz 2'001 − 2*n rozwiązań dla x = 1'000 masz 1 rozwiązanie tak samo dla x<0 (albo zwyczajnie *2 wszystkie rozwiązania dla x>0)

piotr: ale dlaczego dla x=0 x=1 x=2 ?

piotr:

Artur_z_miasta_Neptuna: bo masz nierówność |X| + |Y| ≤ 1'000 gdyby było to równianie to ile by było rozwiązań jakie PARY liczb byś miał ? chociażby (0;1'000) , (1;999), (2;998) , .... (499 ; 501) , ..... , (999;1) i takie same zestawy ale dla liczb ujemnych. tak