 R=4 promień kuli opisanej na ostrosłupie
α=60 zatem ΔEFS jest równoboczny
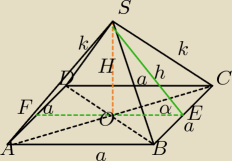
Ostrosłup wpisany w kulę, wszystkie wierzchołki leżą na powierzchni kuli
Koło wielkie kuli jest opisane na ΔACS oraz ΔBDS.
R=4 promień kuli opisanej na ostrosłupie
α=60 zatem ΔEFS jest równoboczny
Ostrosłup wpisany w kulę, wszystkie wierzchołki leżą na powierzchni kuli
Koło wielkie kuli jest opisane na ΔACS oraz ΔBDS.
| AC | |
=2R | |
| sin∡ASC |
| a√3 | ||
H= | ||
| 2 |
| 1 | ||
k2=a2+( | a)2 | |
| 2 |
| 5 | ||
k2= | a2 | |
| 4 |
| 5 | 5 | 5 | ||||
(a√2)2= | a2+ | a2−2* | a2cos∡ASC | |||
| 4 | 4 | 4 |
| 1 | ||
cos∡ASC= | ||
| 5 |
| 1 | ||
sin2∡ASC=1− | z jedynki trygonometrycznej | |
| 25 |
| 2√6 | ||
sin∡ASC= | ||
| 5 |
| AC | |
=2R=8 | |
| sin∡ASC |
| 2√6 | 16√6 | |||
AC=8* | = | |||
| 5 | 5 |
| 16√6 | ||
a√2= | ||
| 5 |
| 16√3 | ||
a= | ||
| 5 |