dziedzina adaś: Oblicz dziedzinę

5x−2
3x2+4

	4
x2= −
	3

D=R dlaczego R? ,skoro nie ma takich liczb rzeczywistych co spełniałyby takie równanie.

ICSP: a jak wyglądała by dziedzina w przypadku :

5x − 2
2x − 3

adaś: 2x−3≠0 2x=3

	2
x=
	3

Bo żadna nie daje liczby równej zero w mianowniku więc D=R ?

Letta: mianownik musi być różny od zera Więc x² musi być różny od −4/3, a wiemy, ze cokolwiek podniesiemy do ² da nam liczbę dodatnią, więc dlatego D=R

adaś:

	4
x2=−		,dlaczego nie jest to równanie z brakiem rozwiązań czyli sprzeczne?
	3

na przykład tutaj jest sprzeczne bo 0 nie jest równe 11 https://matematykaszkolna.pl/strona/1168.html

ICSP:

5x−2
2x−3

	2		2
2x − 3 ≠ 0 ⇒ x ≠		⇒ x ∊ R \{		}
	3		3

z dziedziny wyrzuciłem x dla którego mianownik się zerował. W twoim przykładzie :

5x−2
3x2 + 4

3x² + 4 ≠ 0 ⇒ 3x² ≠ − 4 ⇒ x ∊ R bo żadna liczba podniesiona do kwadratu nie da liczby ujemnej.

adaś:

	4
tak samo dowolna liczba podniesiona do kwadratu nie da nam −
	3

adaś:

	2		2
dlaczego wyrzuciłeś		? jak podstawie do mianownika te		to mianownik nie da nam
	3		3

zera

adaś: ?

asdf: @adaś

3		2
	, nie
2		3

adaś:

	4
rzeczywiście dzięki asdf ,ale ja nadal nie rozumiem dlaczego dziedzina x2= −		to R.
	3

	4
nie ma takiej liczby która po podniesieniu do kwadratu da nam −		czyli równanie
	3

sprzeczne, tak samo jest tutaj https://matematykaszkolna.pl/strona/1168.html 0=11 sprzeczność

Piotr: rozumiesz, ze nie wolno dzielic przez 0 ? rozumiesz, ze w mianowniku nigdy nie wyjdzie 0 ? to znaczy ze kazda liczbe mozesz wstawic do tego wyrazenia, dziedzina sa wszystkie liczby rzeczywiste !

asdf: wyznacz dziedzinę równania:

x2 −1
x2 + 1

a tu jaką dałbyś odpowiedź?

adaś: x²+1≠0 x²≠ −1 także bym dał odpowiedz D=R , nie ma liczb które dawały by zero.

adaś: Wyznacz dziedzinę x²+9≠0 x²= −9 czyli także D=R ,prawda?

Piotr: i dobrze ! wszystkie liczby rzeczywiste mozna wstawiac !

asdf: no widzisz jakie to proste

Mateusz: ekhem czy cokolwiek podniesione do kwadratu da ci ujemną liczbe proponuje sprawdzić

Piotr: a jakie jest rownanie/wyrazenie ?

Piotr: Mateusz i²= −1

Mateusz: No zakładając że mamy do czynienia ze zbiorem liczb zespolonych swoja drogą liczby zespolone są proste a liczby rzeczywiste są urojone

adaś: A powiedzcie mi kiedy jest równanie sprzeczne? Na przykład kiedy wyznaczam jakąś dziedziną to mogę mieć równanie sprzeczne?

Piotr: rozrozniaj co to dziedzina a co to rownanie ! rownanie jest sprzeczne gdy nie ma rozwiazania.

asdf: NIE STWIERDZAM LECZ PYTAM:

√−x + 1
√x − 2

może być?

Piotr: ale o co pytasz ?

adaś: Mam takie wyrażenie

5x+2y−20x−8y
	=0
5x−2y

co z nim mam zrobić dalej?

asdf:

√−x + 1
	= 0
√x − 2

czy to równanie jest sprzeczne

Mateusz: Właśnie moja uwaga byłą skierowana do adasia żeby sobie to przyswoił bo z tego co widać jest początkujący w tych sprawach.

Piotr: @asdf a wyznacz dziedzine

asdf: @adaś pigor już Ci napisał rozwiązanie, podstawiając za x ⇒ y...Takim tropem jak ty chcesz to zrobić będzie trudne

asdf: @Piotr D ∊ ∅ ?

Piotr:

adaś: według mnie to D=R\{2}

asdf: lud D ∉ R

asdf: oj Adaś, ty to chyba nie uczysz się na błędach

adaś: Jaka jest ta dziedzina w przykładzie co podałeś ASDF ?

Piotr: @asdf nie kombinuj za duzo @adaś trzeba rozwiazac −x+1 ≥0 i x−2>0

asdf: uciekła i jej nie ma

asdf: @Piotr chciał równanie sprzeczne to ma...Tylko chyba takim przykładem to można namieszać co niektórym w głowie

adaś: poważnie jak jest dziedzina ? bo się już gubię

Piotr: @adaś milion razy bylo ze nie wolno dzielic przez 0 i ze liczba pod pierwiastkiem stopnia parzystego ≥0

asdf: @adaś masz tu kolejne równanie sprzeczne:

x
	= 0
x

Piotr: dziedzina tego co podal @asdf jest zbior pusty. nie ma takiej liczby ktora moglbys podstawic w miejsce x. wniosek : rownanie sprzeczne. brak rozwiazan.

Piotr:

x
	=0 rownanie nie ma rozwiazania ale D=R\{0}
x

adaś: Piotr, jak bym podstawił dwa w miejsce x to bym miał pierwiastek z 0 ,to było by to większe bądź równe 0 , prawda?

asdf: @adaś daj swoje obliczenia to się zobaczy gdzie robisz błąd

Piotr: w mianowniku nie moze wyjsc 0 to po pierwsze, po drugie musisz patrzec na cale wyrazenie a nie tylko mianownik. ogolnie to tak √0=0.

adaś:

	√−x+1
a kiedy to równanie nie było by sprzeczne		=0 ?
	√x−2

Piotr: @adaś zawsze jest sprzeczne ! bo nie nie ma x, ktory moglys tam wstawic !

asdf: @adaś Daj swoje obliczenia jak rozwiązujesz dziedzinę...bo ty chyba nie wiesz o co chodzi

adaś: Czyli w tym przykładzie będzie D=∅ , czyli inaczej równanie sprzeczne mogę zapisać?

Piotr: juz pisalem, ze @adaś trzeba rozwiazac −x+1 ≥0 i x−2>0

asdf: a wiesz dlaczego tak jest, że D = zbiór pusty?

Piotr: no mozesz..

adaś: ASDF , dlatego że nie nie ma takich x co by były większe bądź równe zero , jak byśmy za iksa wstawili 2 to by wyszło 0 a nie może, gdybyśmy za iksa wstawili 5 to by wyszła liczba ujemna a nie może wyjść

adaś: prawda?

asdf: −x + 1 ≥ 0 ⇔ −x ≥ −1 ⇔ x ≤ 1 x − 2 > 0 ⇔ x > 2 −x + 1 ≥ 0 U x − 2> 0, brak części wspólnej

adaś: To co ja napisałem jest źle ? I co z tego że brak części wspólnej? To co narysowałeś to dlaczego jest zbiór pusty? Przecież przedział to (−∞;1> U (2;∞)

asdf: nic nie napisałeś źle, napisałeś to tak "łopatologicznie", tu masz na wykresie.. SUMA TO NIE CZĘŚĆ WSPÓLNA! ILE RAZY TRZEBA BĘDZIE TO TOBIE POWTARZAĆ?!

adaś: no ale mam takie coś narysować x≤1 ,x>2 , to jaki będzie przedział bo już nic nie rozumię

asdf: mój błąd, powinien być taki zapis: −x + 1 ≥ 0 ∩ x − 2> 0

adaś: ale po czym poznajesz że to ma być część wspólna akurat?

asdf: Przeczytaj swój post z 14³⁷ i się dowiesz

adaś: aha Ty mi tylko to wizualnie pokazałeś ,ale wcale tak nie muszę robić prawda?

adaś: określ dziedzinę, znowu mam problem i nie rozumiem f(x)= √x²+√−x² √x² − zbiór R ,to rozumiem a odpowiedź mam że D={0}, dlaczego tak ?

asdf: Część wspólna

asdf: Próbuj notować sobie lub w jakikolwiek sposób zapamiętywać to, jak co się robi...bo chyba masz problemy z pamięcią albo koncentracją

adaś: boże ja nie wiem już o co chodzi z tą częścią wspólną , jak dojść że D={0}, to co ja wiem jak bym miał wyznaczać tutaj dziedzinę to: √x²≥0 √−x²≥0 w pierwszym tylko zbiór R a w drugim to nie wiem

adaś: drugim także bym dam zbiór R ,pownieważ każdą liczbę ujemną czy dodatnią podniesioną do kwadratu da nam liczbę większą od zera

adaś: więc nie wiem dlaczego D={0}

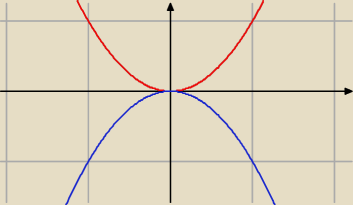
asdf: narysuj sobie dwie takie parabole i zobacz w którym punkcie się stykają inaczej: x² ≥ 0 <<−−−−−−−−−to już tak zostawiamy −x² ≥ 0 || *(−1) ⇔ x² ≤ 0

adaś: ale w pierwszym mam x²≥0 ,więc dla np, 1 czy 2 spełnia się ta nierówność

asdf: MASZ WYZNACZYĆ CZĘŚĆ WSPÓLNĄ A NIE PODSTAWIAĆ JAKIEŚ LICZBY!

adaś: nie wiem dlaczego akurat część wspólna, nawet nie myślę o części wspólnej przy wyznaczaniu jakiej kolwiek dziedziny, jak mam taki przykład f(x)= √x²+√−x² , to robię warunek że muszą być ≥ x²≥0 −x²≥0 x²≤0 , dziedziną są liczby większe bądź równe zero co wynika z warunku" ≥0"

adaś: czyli w x²≥0 , mogą być każde liczby bo zawsze będą większe , w x²≤0 , może być tylko liczba zero , więc nie wiem jak dziedziną zrobić skoro mam w jednym wyrażeniu wszystkie liczby rzeczywiste a w drugim tylko 0 , czyli według zbiór wartości powienien być R

asdf: masz wyznaczyć część wspólną....

adaś: ale po czym to poznajesz? Ja sądzę że matematykę trzeba rozumieć a zapamiętywać poszczególne przypadki. Np. f(x)=√5−x+√x+√5−x , jak tutaj wyznaczam dziedzinę to rozumiem dlaczego D=<0;5> ponieważ z tego przedziału suma daje nam tylko wartości ≥0 , a w tym f(x)=√x²+√−x² ,robię podobnie stawiam że ta cała suma musi być ≥0 , i to się spełnia dla liczb rzeczywistych,więc nie wiem dlaczego D={0}

asdf: −x²≥ 0 || * (−1) PAMIĘTAJĄC O ZMIENIE ZNAKU! x² ≤ 0 zrozumiałeś tamto, a nie potrafisz tego...tutaj też masz część wspólną, który jest jedynie 0..

adaś: chyba skumałem dlaczego tylko zero, bo ten znak zmieniłem ,dzięki że przetrwałeś ze mną do końca

asdf: nie było łatwo , myślałem,ze już nie zrozumiesz...