wyznacz ekstrema lokalne.zbadaj monotoniczność funkcji. ania: f(x)=^x5₅−^x3₃+2

Basia: policz najpierw f'(x) podaj wynik

ania: Nie wiem czy to dobrze liczę 4x³−2x

Basia: f'(x) = ¹₅*5x⁴ − ¹₃*3x² = x⁴ − x² = x²(x²−1) = x²(x−1)(x+1) znajdź teraz miejsca zerowe f'(x)

ania : f'(x) = 0 x²(x−1)(x+1) = 0 x² = 0 x = 0 x−1 = 0 x = 1 x+1 = 0 x = −1 x = 0,1,−1 ? Co dalej ?

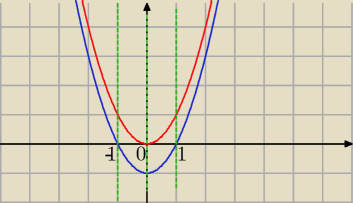
Basia: teraz rysujesz wykres pochodnej wystarczy, że narysujesz oddzielnie y = x² i y = x²−1 z wykresu odczytujesz jak zachowuje się pochodna (chodzi o znak) i na tej podstawie określasz jak zachowuje się funkcja x∊(−∞;−1) ⇒ f'(x) = (+)*(+) = (+) > 0 ⇒ f.↗ x∊(−1;0) ⇒ f'(x) = (+)*(−) = (−) < 0 ⇒ f.↘ x∊(0;1) ⇒ f'(x) = (+)*(−) = (−) < 0 ⇒ f.↘ x∊(1;+∞) ⇒ f'(x) = (+)*(+) = (+) > 0 ⇒ f.↗ jak widać w p−cie x=0 pochodna nie zmienia znaku czyli nie ma tam ekstremum dla x= −1 masz maksimum , bo najpierw rośnie a potem maleje(↗↘) dla x=1 masz minimum, bo najpierw maleje a potem rośnie (↘↗) jeżeli trzeba to policz f_max = f(−1) i f_min = f(1)

ania: DZIĘKI WIELKIE POZDRAWIAM