trapez równoramienny Krzychu: dany jest trapez A(7,−4) B(7,10) C(6,5) D(6,1). Oś symetrii to prosta o równaniu y=3. Jak obliczyć środek okręgu opisanego, za pomocą wektorów?, bo ja zrobiłem r=|BS|=|CS| i z równania na odcinki.

mcjng: podbijam

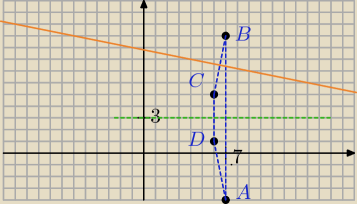
Mila: środek okręgu opisanego leży na przecięciu symetralnych boków. y=3 symetralna CD i AB Środek CB:

	6+7		10+5
(xs;ys)=(		;		)=(6,5;7,5)
	2		2

CB^→[1,5] symetralna CB: (piszę korzystając z wektora CB) x+5y+C=0 6,5+5*7,5+C=0 C=−44 x+5y−44=0 podstawiamy y=3 x+5*3=44 x=29 S=(29,3)

Mila: Posprawdzaj, bo przyszli goście i znikam na chwilę.

Krzychu: Wynik ok dzięki. . gdzie mogę znaleźć ten wzór: symetralna CB: (piszę korzystając z wektora CB) CB[1,5] x+5y+C=0

Krzychu: ?

Mila: Dla dowolnego C∊R prosta Ax+By+C=0 jest prostopadła do wektora w^→=[A,B] W naszym przypadku w^→=[1,5] stąd x+5y+C=0 to jest prosta prostopadła do CB, ale my chcemy, aby przechodziła przez środek CB, to podstawiamy do równania wsp.środka CB.

logika: Ax+By+C=0 i za A,B podstawiasz odpowiednio 1 i5 ( CB→[1,5])