wykres funkcji wymiernej :) gr: Witam Czy mógłby mi ktoś wytłumaczyć jak będzie wyglądał wykres funkcji: 6/(|x| − 3)?

ICSP:

6
|x| − 3

Rysujesz wykres funkcji :

	6
f(x) =		tylko po prawej stronie osi OY a następnie rysujesz lewą stronę symetrycznie
	x − 3

	6
względem osi OY. i otrzymujesz f(x) =
	|x|−3

gr: dzięki za odpowiedź Wiem, że tak to będzie wyglądać, ale mam nieco inne pytanie. Skoro odejmujemy 3, to mamy taki wektor: [0,3] Dla dodatnich przesuwamy w prawo, a dlaczego już dla ujemnych przesuwamy o wektor w prawo?

gr: poprawka: Dla dodatnich przesuwamy w prawo, a dlaczego już dla ujemnych przesuwamy o wektor w lewo?

ICSP:

	a
f(x) =		+ c
	x − b

wiec mamy wektor : [b ; c] teraz nie rozumiem troszkę twojego pytania

ICSP: jakich ujemnych Daj jakiś przykład

gr: dla ujemny x−ów. Weźmy: x = −5 Hmm, może ja źle rysuję te wykres Robię tak: 1. Rysuję "podstawowy wykres" typu 4/x. A potem przesuwam go o odpowiedni wektor. I tak właśnie robiłem w tym zadaniu. Tzn. Liczyłem np. dla x=3. wychodziło mi ileś tam, a punkt rysowałem o 3 jednostki w prawo. Tak samo robiłem dla ujemnych, ale nie wyszło mi symetryczne

ICSP:

	6
Najpierw narysowałeś wykres f(x) =		a później dopiero zacząłeś go odbijać ?
	x − 3

gr: ale jak mogę go narysować w prostej postaci, a dopiero potem odbijać skoro pod wartością bezwzględną nie jest wszystko tylko jeden czynnik. (x)

ICSP:

	6
zapis f(x) =		oznacza że wykres został "nadpisany"(cześć wykresu w ćwiartce II oraz
	|x| −3

III została "nadpisana" przez wykres który leży w ćwiartce I oraz IV) względem osi OY. Zapisujemy to jako f(|x)

	6
zapis f(x) = |		| oznacza ze wykres został odbity względem osi OX. Zapisujemy |f(x)|
	x −3

W obydwu przypadkach najpierw rysujemy ten wykres. a Później go odpowiednio przekształcamy.

Mila:

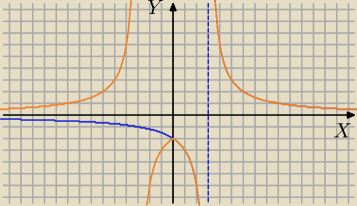
	6
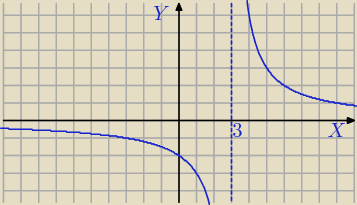
f(x)=		niebieski, narysuję go jeszcze na innym wykresie.
	x−3

	6
g(x)=		pomarańczowy.
	|x|−3

(niebieska część wykresu odpowiadająca dodatnim x−om została odbita symetrycznie względem OY, natomiast odpowiadająca ujemnym zostaje pominięta) Przeczytaj jeszcze co Ci napisał ICSP .

Mila: Porównaj teraz wykresy.

	6
f(x)=
	x−3