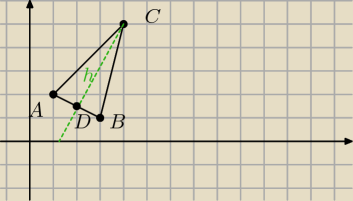
Geometria agatttt: Oblicz dlugosc wysokosci trojkata ABC poprowadzonej z wierzcholka C gdzie A=(1,2), B(3,1), C(4,5) i napisz rownanie wysokosci poprowadzonej z wierzcholka C. Z gory dziekuje

Skipper: − napisz równanie prostej przechodzącej przez A i B

	1
− wysokość leży na prostej o współczyniku −		− przechodzącej przez C
	a

− miarę wysokości policzysz jako odległość punktu C od prostej przechodzącej przez A i B

dero2005: współczynnik kierunkowy prostej AB

	yB−yA		1−2		−1
aAB =		=		=		= −12
	xB−xA		3−1		2

równanie prostej przechodzącej przez punkty A i B y_AB = a_AB(x−x_A)+y_A = −¹₂(x−1)+2 = −¹₂x + ⁵₂ współczynnik kierunkowy wysokości h (prostej CD) a_CD*a_AB = −1 a_CD = 2 równanie wysokości h y_CD = a_CD(x−x_C) +y_C = 2(x−4)+5 = 2x−3 długość wysokości h (odległość punktu od prostej)

	|AxC + ByC + C|
d =
	√A2 + B2

y = −¹₂x+⁵₂ równanie kierunkowe x + 2y − 5 = 0 równanie ogólne A = 1 , B = 2 , C = −5

	|1*4 +2*5 − 5|		9√5
d =		=
	√12 + 22		5