Help! POMOCY!!: wykaz , ze jezeli katy wewnetrzne trojkata spelniaja warunek sinα = 2cosδsinβ to ten trojkat jest rownoramienny

imię lub nick: jak to udowodnić? ? ?

@Basia: Pomagam.

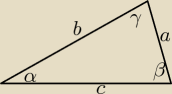
@Basia: Napisałam γ zamiast δ. To niczego nie zmienia. sinα=2cosγsinβ α+β+γ=180 α=180−(β+γ) sinα=sin[180−(β+γ)] = sin(β+γ) = sinβcosγ+sinγcosβ sinβcosγ+sinγcosβ = 2sinβcosγ sinγcosβ = sinβcosγ sinβcosγ − sinγcosβ=0 sinβcosγ − sinγcosβ = sin(β−γ) stąd: sin(β−γ)=0 ⇒ β−γ=0 ⇒ β=γ ⇒ trójkąt jest równoramienny Przepraszam, że tak długo to trwało, ale musiałam coś zrobić w domu.

POMOCY!!: dzieki wielkie

POMOCY!!: sinβcosγ+sinγcosβ << mam tylko pytanie skad sie to wzielo ?

Eta: Podam też inny sposób: ze wzoru sinusów mamy:

a		a
	= 2R to sinα=
sinα		2R

b		b
	=2R to sinβ=
sinβ		2R

ze wzoru kosinusów wyliczamy cosγ

	a2 +b2 − c2
cosγ=
	2ab

teraz podstawiając do danej równości: sinα= 2*cosγ*sinβ otrzymamy:

a		a2 +b2 − c2		b
	= 2*		*		( skracamy 2 i b)
2R		2ab		2R

po przekształceniu 2Ra² = 2R(a² +b² −c²) i skróceniu przez 2R otrzymamy: a² = a² +b² − c² => b² = c² => b= c więc trójkąt jest równoramienny o ramionach b= c