function (searchElement /*, fromIndex */ ) {
"use strict";
if (this ==
null) {
throw new TypeError();
}
var t = Object(this);
var len = t.length >>> 0;
if (len === 0) {
return -1;
}
var n = 0;
if (arguments.length > 0) {
n = Number(arguments[1]);
if (n != n) {
// shortcut for verifying if it's NaN
n = 0;
} else if (n != 0 && n !=
Infinity && n != -Infinity) {
n = (n > 0 || -1) *
Math.floor(Math.abs(n));
}
}
if (n >= len) {
return -1;
}
var k = n >= 0 ? n : Math.max(len - Math.abs(n), 0);
for (; k <
len; k++) {
if (k in t && t[k] === searchElement) {
return k;
}
}
return -1;
}
no chyba ze rajcują cie takie
krzaczki 
| 1 | ||
u'= | , v=x | |
| x2+1 |
| x | ||
... x * arctg x − ∫ | dx | |
| x2+1 |
| x | ||
Pomocniczo liczymy całkę ∫ | dx (np przez podstawienie x2+1=t) | |
| x2+1 |
| x | ||
∫ | dx = ... | |
| x2+1 |
| 1 | ||
xdx= | dt | |
| 2 |
| 1 | dt | 1 | 1 | |||||
... | ∫ | = | ln(t) + C = | ln(x2+1) + C | ||||
| 2 | t | 2 | 2 |
| x | 1 | |||
∫arctg x dx = x * arctg x − ∫ | dx = x * arctg x − | ln(x2+1) + C | ||
| x2+1 | 2 |
| 1 | 1 | π | 1 | |||||
∫01 arctg x dx = arctg 1 − | ln(2) − 0 + | ln(1) = | − | ln(2) ≈ | ||||
| 2 | 2 | 4 | 2 |
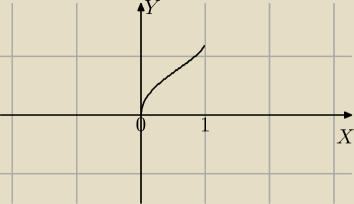Na kolokwium nie masz wolframa, to przybliżony wykres tak możesz wykonać.
arcsinx ma wartości nieujemne dla x∊<0,1> i jest funkcją rosnącą w przedziale
y=√arcsinx też f. rosnąca
arcsin0=0 ⇒√arcsin0 =0 punkt(0;0)
| 1 | π | π | 1 | |||||
arcsin | = | ⇒√arcsin | ≈0,7 punkt( | ;0,7) | ||||
| 2 | 6 | 6 | 2 |
| π | π | |||
arcsin1= | ⇒√arcsin | ≈1,3 punkt(1; 1,3) | ||
| 2 | 2 |