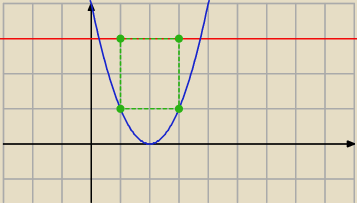
Geometria vexetariano: Dwa wierzchołki A i B prostokąta leżą na paraboli o równaniu y=x²−4x+4, a pozostałe dwa C i D na cięciwie paraboli wyznaczonej przez prostą y=3. Udowodnij, że największa wartość pola prostokąta ABCD wynosi 4.

Artur_z_miasta_Neptuna: może być to prawdą tylko gdy się założy, że wierzchołki AB leżą "pod" wierzchołkami CD (innymi słowy ... że prostokąt nie ma wierzchołków na paraboli NAD prosta y=3) a takiego założenia tutaj brakuje. f(x) = (x−2)² jako a_x oznaczmy długość podstawy prostokąta a_x ∊ (0; czegoś mniejszego od 4) b_y − oznaczmy jako wysokość tegoż prostokąta b_y dany jest wzorem

	ax		ax2
by = 3 − ((2−		) − 2)2 = 3 −
	2		4

	ax2		ax3
Pprostokąta = ax * (3 −		) = 3ax −
	4		4

musisz wykazać, że dla a_x z przedziału (0; czegoś mniejszego od 4) to 4 jest największą wartością jaką przyjmuje ten wielomian a to się z kolei sprowadza do wyznaczenia WIERZCHOŁKA tejże funkcji

Skipper: ... czy napewno Arturze ... skoro leżą na cięciwie ... to pozostałe nie mogą być nad prostą ...

Artur_z_miasta_Neptuna: fakt ... słowo cięciwa w głowie mi się zamieniał na prostą