ggg mrrr: Proszę o pomoc nie wiem jak zowiązać następujące zadania: sinx + cosx = 0 x∊(0, 2π). x³ + 1 < 0 naszkicuj przedział opisany dwiema równaniami

⎧	y = −x
⎩	y > x2 − 1

loitzl9006:

	π
cos x = sin(x+		)
	2

	π
sinx + sin(x+		) = 0
	2

ze wzoru na sumę sinusów

	π		π
2sin(x+		)*cos(−		)=0
	4		4

	π		π		√2
cos(−		)=cos(		)=
	4		4		2

	π
√2sin(x+		)=0
	4

	π
sin(x+		)=0
	4

	π
x+		= π
	4

	3π
x=
	4

−−−−−−−−−−−−−−−−−−−−−−−−−−−− x³+1<0 wzór skróconego mnożenia na sumę sześcianów: a³+b³=(a+b)(a²−ab+b²) zatem (x+1)(x²−x+1)<0 wielomian x²−x+1 jest nierozkładalny, zatem rysujemy "wężyk" i otrzymujemy rozw: x∊(−∞;−1) −−−−−−−−−−−−−−−−−−−−−−−−−− Co do trzeciego zadania, to szukanym przedziałem będzie fragment prostej y=−x leżący powyżej paraboli x²−1.

Godzio: Pokaże inny sposób dla pierwszego:

	π
cosx = − sinx, ale −sinx = sin(−x) = cos(−x −		)
	2

	π		π		π
cosx = cos(−x −		) ⇒ x = −x −		+ 2kπ ⇒ x = −		+ kπ
	2		2		4

	3π
Zatem dla danego przedziału: x =
	4

mrrr: Właśnie mam problem bo nie rozumiem jak liczyć zadania z trygonometrii stosując zapis radianowy. Podrzuccie jakiegoś linka .

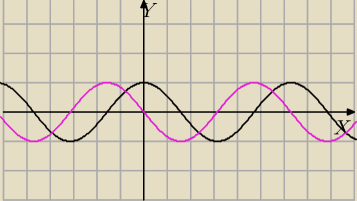
Mila: Godzio, chyba jakąś literówkę zrobiłeś. wykresy − cosx − czarny (−sinx) − różowy ( potrzebne przesunięcie)

loitzl9006:

	3π		7π
mi jeszcze jednego rozwiązania zabrakło, oprócz x=		ma być jeszcze x=		.
	4		4

Co do zapisu radianowego to trzeba zapamiętać, że 180 stopni to π radianów

	π
czyli 90 stopni to
	2

	π
45 to		itd
	4

Mila: Zgadzam się z Tobą Loitz.

Godzio: Mila, po prostu rozwiązywałem równanie, tylko pominąłem już formalności sinx + cosx = 0 ⇒ cosx = − sinx

Mila: NO, teraz wiem o co Ci chodziło.Pozdrawiam. Zobacz jutro zadanie ze styczną, rzuć życzliwie oczkiem.Dobranoc.

PW: @Loitz9006: Wszystko pięknie w sensie pomysłu i przekształceń. Gubisz jednak rozwiązania w wyniku typowego błędu.

	π		π
Doszedłeś do sin(x +		) = 0 i wyciągasz wniosek, że x+		=π. Tak, ale nie ą to
	4		4

	π
wszystkie rozwiązania. Dziedziną funkcji sin(x +		) nie jest zadany przedział (0,2π),
	4

	π		π
lecz (		,2π+		), a tam sinus zeruje się dwa razy.
	4		4

Dlatego dla początkujących bezpieczniejsza jest wersja z podzieleniem przez cosx obu stron równania. Sprawdzamy najpierw, że można podzielić (x, dla których cox=0 nie są pierwiastkami). Po podzieleniu mamy tgx=−1. Narysowanie wykresu funkcji tangens na przedziale (0,2π) pozwoli uniknąć zgubienia pierwiastków − widać wtedy, że są dwa. To tak dla mrrr (wiem, że już widzisz błąd, ale nie wytłumaczyłeś, skąd się wziął.).