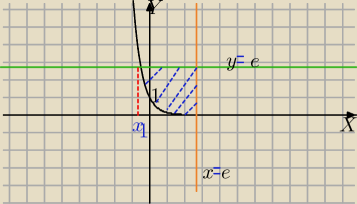
Całki oznaczone - pole Tiamat: Sporządź rysunek i oblicz pole obszaru ograniczonego liniami: y = e^−2x y = e x = e Po pierwsze − jak dobrze wykonać rysunek tych lini? Mniej więcej wiem jak to ma wyglądać, ale potrzeba mi czegoś dokładnego raczej. Po drugie zacięłam się przy: e^−2x = e to jest w ogóle możliwe? Proszę o pomoc w rozwiązaniu: )

Ajtek: Masz prostą y=e oraz jakąś krzywą y=e^−2x

	1
A ta równość e−2x=e jest prawdziwa gdy −2x=1 ⇒x=−
	2

Vizer: Wcale nie trzeba dokładnego rysunku. Rysunek pomaga stwierdzić, który wykres jest wyżej, który niżej oraz na jego podstawie można zobaczyć, które funkcje sie ze sobą przecinają. Co do Twojego problemu: e^−2x = e¹ −2x = 1

	1
x = −
	2

Tiamat: Ok, dzięki teraz to zorumiem: )

Tiamat: Czyli calka z tego będzie tak lecieć: ∫e dx − ∫e^−2x dx = e−e^−2e2 − [e−e¹] = e−e^−2e2 − 0 ? Nie wiem jak wstawić tam −2e² zamiast −2e2 : )

Vizer: Coś tu jest mocno schrzanione. Zacznijmy od tego skąd wzięłaś e ² i gdzie granice całkowania

Tiamat: Hmm, przepraszam na początku przy danych jest bład: nie x=e ale ma być x= e² Stąd pewnie wynika dalsze zamieszanie

Vizer: To dalej jest nie za fajnie ... Liczyłaś taką całkę? Bo z Twojego zapisu ciężko coś wywnioskować, a wynik jest zły. ∫^e2₀(e − e^−2x)dx ?

Tiamat: Hmm, faktycznie no wygląda inaczej, zamiast zera miałam −¹₂ reszta tak samo. Potem rozbiłam na dwie calłki, bo mi wygodniej tak liczyć.

Tiamat: Zasadniczo z moim małym rysunkiem nie zgadza się tylko znak przy ¹₂

Ajtek: Dlaczego dolna granica całkowania jest 0?

Vizer:

	1
Nie no ok, zasugerowałem się pionową ośką i dałem dolną granicę 0, ma być oczywiście −		,
	2

przepraszam za zamieszanie

Vizer: Ale dalej nie wiem czy całka dobrze policzona. Ile jest ∫edx i ∫e^−2xdx ?

Ajtek: Na mnie się nie patrz, całeczki sobie próbuje przypominać

Vizer: Ale miałeś rację, rzeczywiście strzeliłem gafę z tą dolna granicą A pytanie jest do Tiamat, bo wynik mi się nie zgadza z jej wynikiem.

Ajtek: Jak widzisz z granicami całkowania sobie radzę, lecz dalej jest kicha .

Vizer: Przypomnisz sobie szybko jak kiedyś to ogarniałeś, mój ojciec kiedyś studiował elektrotechnike, to całki musiał rzecz jasna umieć rozwiązywać, nie pamiętał, po 20 latach, jak się je rozwiązuje, ale po krótkim wstępie, paru przykładach zaczął sobie szybko przypominać

Mila:

	1
x1=−
	2

	1
−1/2∫e(e−e−2x)dx=[ex+		e−2x]−1/2e=
	2

	1
=e2+		e−2e
	2

Ajtek: Witaj Mila x=e² jest górną granicą .

Vizer: Mila była poprawka, że x = e²

Tiamat: No przecież z e w różnych kombinacjach zawsze wychodzi to samo e : ) Czyli moja całka ostatecznie wychodzi tak: ∫e dx − ∫e^−2x dx = e − e^−2x potem podstawiam za x = e² i x= −¹₂ −2x = −2e² i −2x = 1 <− to same potęgi bo nie wiem jak zapisać przy e

Vizer: ∫e dx − ∫e^−2x dx = e − e^−2x Fałsz nad fałszem, bo my całkujemy po x po pierwsze, po drugie pewnie pomyliłaś sobie z tym ∫e^xdx = e^x + C

Tiamat: No to ja już zgłupiałam: D To jak to ma w takim razie wyglądać? Właśnie używałam tego wzorku.

Tiamat: Czyli co, mam traktować e jak normalną liczbę? Myślałam, że już to zaczaiłam

Vizer: Bo Ty masz w pierwszym ∫edx = ( tu e jest stałą wyłączamy przed znak całki ) = e∫dx = ex + C W drugim rzeczywiscie będziemy korzystać ze wzoru ∫e^xdx = e^x + C, ale nie tak od razu: ∫e^−2xdx = * t = −2x dt = −2dx

	1
−		dt = dx
	2

	1		1		1		1
* = ∫et * (−		)dt = −		∫etdt = −		et = −		e−2x + C
	2		2		2		2

Teraz jasne?

Tiamat: Ok to pierwsze nie mam zastrzezeń, mam pytanie do drugiego e do potęgi. Na tej stronce dt=dx jest dziwnie wytłumaczone i ja generalnie gdybym chciała to policzyć to mi wychodzą bzdury i jestem zablokowana. t=−2x dt = −2xdx −¹₂dt = xdx Oto mój problem, wytłumaczysz skąd taka różnica?

Vizer:

	d
t = −2x − teraz różniczkujemy obustronnie czyli mnożymy obustronnie po		(pochodna po x)
	dx

dt		d
	=		(−2x)
dx		dx

dt
	= −2 /*dx
dx

dt = −2dx

	1
−		dt = dx − wynik
	2

Tiamat: Ok, dzięki poćwiczę to: ) W ogóle dzięki za wszystko mam nadzieję, że zdam: )

Vizer: Spoko, jak masz jeszcze jakieś wątpliwości z jakimiś innymi zadaniami to pisz śmiało

Tiamat: Oki: ) może to: y=arcsinx x=0 y=^π₆ arcsinx = ^π₆ x= ¹₂ nigdy nie wiem jakie mają wartości arc cosie : D całka: ∫ arcsinx − ^{π}[6} dx = xarcsinx + u{1}₂x²arcsinx − u{πx}[6} aha, granice to: x= ¹₂ i x=0 czyli ostatecznie wyszło mi:

9π
48

Tylko nie wiem czy to dobrze jest: )

Vizer: Przepisz tę całkę jeszcze raz, bo trudno się z tego odczytać.

Tiamat: oj coś mi się podziało przy całeczce... ∫arcsinx − ^π₆ dx = xarcsinx + ¹₂ x² arcsinx − ^xπ₆ z tym, że wynik końcowy − z nim chyba przesadziłam i ze sprowadzaniem do wspólnego mianownika:3

Vizer: Po pierwsze chyba powinno być :

	π		π
∫(		− arcsinx)dx, bo wg mojego rysunku		jest wyżej od arcsinx na przedziale od 0
	6		6

	1
do
	2

I przedstaw mi jak liczysz ∫arcsinxdx, bo coś mi się tu nie zgadza.

Tiamat: Okk, faktycznie jest wyżej, miałam dylemat które pole mam liczyć w ogóle bo jak nie miałam ¹₂ to miałam dwa możliwe pola. samą całkę arcsinx?

	1
∫ 1 arcsinx dx = l f=arcsinx f' =		g' =1 g=x l =
	√1−x2

	1
x arcsin − ∫		x dx =
	√1−x2

x arcsinx − arcsinx ¹₂x² tadam, koniec. Jest dobrze?

Vizer:

	x
∫		dx jak liczyłaś tę całkę?
	√1 − x2

Tiamat: Nie wiem, już mam chyba zamiast mózgu kisiel... Zaraz policzę jeszcze raz, ale to chyba przedostatnie zadanie na dziś...

Tiamat: Juz wiem o co Ci chodziło, źle to policzyłam bo potraktowałam tą całkę jakby to było dodawanie i odejmowanie − czyli każdą z osobna. W tej chwili chyba i tak już więcej policzyć nie dam rady.

Vizer: Podstawienie za t = √1 − x² spróbuj.

Tiamat: ∫arcsinx dx = xarcsinx − √1−x² + C ok, czyli: xarcsinx − √1−x² − ^π₆x jest wynikiem?

loitzl9006: Mały błąd masz. ∫arcsinx dx = ... u= arcsin x v'=1

	1
u'=		v=x
	√1−x2

	x
... = x * arcsin x − ∫		dx
	√1−x2

	x
∫		dx = ...
	√1−x2

1−x² = t −2xdx = dt

	1
−xdx =		dt
	2

	1
xdx = −		dt
	2

	1		1
... = −		∫		dt
	2		√t

	1
W całce masz takie coś jak		. Przypominamy sobie zamianę pierwiastka na potęgę:
	√t

√t = t^1/2 i jeszcze taką własność:

1
	= t−a
ta

zgodnie z tym wszystkim

1		1
	=		= t−1/2
√t		t1/2

	1
Zatem ∫		dt = ∫ t−1/2 dt
	√t

i na takie coś mamy wzór:

	tα+1
∫ tα dt =		+ C dla α≠−1
	α+1

u nas α=−1/2, zatem można ten wzór wykorzystać:

	t1/2
∫ t−1/2 dt =		+ C = 2√t + C = 2√1−x2 + C
	1/2

zatem

	x		1		1		1
∫		dx = −		∫		dt = −		* 2√1−x2 + C = −√1−x2 + C
	√1−x2		2		√t		2

czyli

	x
∫arcsinx dx = x * arcsin x − ∫		dx = x * arcsin x − (−√1−x2 ) + C =
	√1−x2

= x * arcsin x + √1−x² + C

	π		1
Teraz liczymy całkę ∫ (		− arcsin x) dx w granicach od 0 do
	6		2

czyli

	π		π
∫ (		− arcsin x) dx =		* x − x * arcsin x − √1−x2 + C
	6		6

wstawiamy granice:

π		1		1		1
	*		−		* arcsin		− √1−14 − 0 + 0 + √1 =
6		2		2		2

	π		π		√3		2−√3
=		−		− √34 + 1 = 1 −		=
	12		12		2		2