pole powierzchni tomek : Witam może mi ktos sprawdzić moje zadanie czy jest ok oblicz całke ∫∫(2x+1)dxdy gdzie D jest trójkątem o wierzchołkach A(0,0) B(2,1) C(−2,1) moje pole powierchni wyszlo mi 2 w miare logiczne jeśli pisałbym to zadanie tutaj zajeło by mi to bardzo dużo czasu, więc jeśli ktoś mógłby mi je sparwdzić to ja może wysle to zadanie zeskanowane bardzo prosze o pozytywna reakcje pozdrawiam

MQ: Mi też wyszło 2 Ale tak dla ścisłości −− to nie jest pole powierzchni, bo pole powierzchni byłoby liczone przez całkę ∬dxdy, a ty masz całkę ∬(2x+1)dxdy

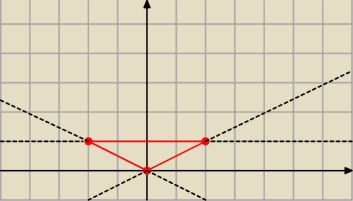
Artur_z_miasta_Neptuna: dzielisz na dwie całki:

	1
1) −2≤x≤0 ⋀ −		x ≤ y ≤ 1
	2

	1
2) 0≤x≤2 ⋀		x ≤ y ≤ 1
	2

1) ∫∫ (2x+1) dxdy = ∫ (2x+1) * [y] dx = ∫ (2x+1)(1+0.5x) dx = ∫ (x² + 2.5x + 1) dx =

	x3		5		8		1
= [		+		x2 + x] =		− 5 + 2 = −
	3		4		3		3

2) ∫∫ (2x+1) dxdy = ∫ (2x+1) * [y] dx = ∫ (2x+1)(1−0.5x) dx = ∫(−x² + 1.5x + 1) dx =

	x3		3		8		7
= [−		+		x2 + x] = −		+ 3 + 2 =
	3		4		3		3

suma = 2 jak widzisz ... aż tyle pisania to nie było

tomek : MQ mam do Ciebie baardzo poważne pytaniei to nie są żadne żarty, pisze w piątek egzamin z matematyki 2 i rozwiązuje zadania lecz nie jestem pewiem czy wykonuje je dobrze, wpisywanie całego zadania na tą strone zajmuje sporo czasu, więc moja prośba brzi czy jest możliwośc jakoś skontaktować sie z Tobą i ja wysyłał bym Ci skany moich zadań, a Ty okresliłbyś czy sa ok pozdrawiam

MQ: Ja niestety akurat w ten i następny tydzień mało mam czasu i rzadko tu bywam, ale wrzucaj tu linki do skanów, a na pewno Artur z miasta Neptuna czy ktoś inny, np ja ci to sprawdzimy, bo to rzadkość, że ktoś coś robi i tylko chce, żeby mu sprawdzić −− lubimy takich.

tomek : mam kolejne zdanie Oblicz ∫∫(2+x)dxdy gdzie D jest trójkątem o wierzchołkach A(0,2) B (−1,−1) C(−2,1) wiem że powinno wyjśc około 4,5 i mi wyszło 18 tylko nie wiem gdzie zrobiłem błąd, poradzicie cos na to 1) −1≤x≤0 ⋀ −2≤y≤3x+2

	3
2) 0≤x≤2 ⋀ −2≤y≤ −		x +2
	2

Z 1) wyszło mi 4 Z 2) wyszło mi 14 na pewno coś tu jest źle

MQ: Wg mnie powinno być:

	1
1) −2<x<−1 ⋀ −2x−3<y<		x+2
	2

	1
2) −1<x<0 ⋀ 3x+2<y<		x+2
	2

tomek : Przepraszam pkt C ma wsp C (2, −1)

MQ: No to walnąłeś się w dolnej granicy y −− powonno być −1, a nie −2: 1) −1<x<0 and −1<y<3x+2

	3
2) 0<x<2 and −1<y<−		x+2
	2

tomek : faktycznie. dopiero teraz to zauważyłem, na rysunku inna skale przykołem na x a inna na y, zaraz policze jescze raz i zobaczymy jak to bedzie wówczas wyglądać

tomek : tak czy siak i tak mi nie wychodzi 1) wyszło 2,5 2 wyszło 6 to i tak za duzo , a Wam

MQ: 1) 2,5 2) 8

tomek : ok wyszło mi tak samo zjadłem minusa , dzięki wielkie za pomoc, mam nadziejeże jescze mi kiedyś pomożesz, a ja jakos Ci sie odwdzięcze

MQ: Na dzisiaj OVER, idę spać.

tomek : jeśli jescze ktos nie śpi to prosze o pomoc w całce ∫(2y + x)dy będzie wynosić [y² + x]y prawda czy nie?

Godzio: y² + xy

Piotr: znasz wolframalpha ?

Piotr: Twój przykład http://www.wolframalpha.com/input/?i=integral+%282y%2Bx%29+dy

tomek : ∫dx∫(2y+x)dy =∫dx[y²+x]y I t onie to samo

Piotr: http://www.wolframalpha.com/input/?i=integral+dx+integral+%282y%2Bx%29dy