parametr
wilk: Dane jest równanie (2cosα−1)x
2−2x+cosα=0 gdzie α∊<0;π>. Dla jakich α równanie to ma dwa
pierwiastki rzeczywiste?
takie warunki dać ?
1) Δ>0
2) 2cosα−1≠0
coś jeszcze ?
Moje obliczenia
cosα=t; −1≤t≤1 α≠
π3
teraz mam
(2t−1)x
2−2x+t=0
Δ=4−4(2t−1)t=4−8t
2+4t
−8t
2+4t+4>0
t
1=1
t
2=−0,5
t∊(−0,5;1)
| | π | |
czyli cosα∊<−0,5;1> i α∊<0;π> zatem α∊(0, |
| ) co dalej lub co zgubiłem bo w odp mam wynik: |
| | 3 | |
17 wrz 18:20
wilk: jakakolwiek podpowiedź ?
17 wrz 18:35
Aga1.: Obliczenia ok, tylko odp. błędna.
−0,5<cosα<1 rozrysuj sobie
17 wrz 18:45
ZKS:
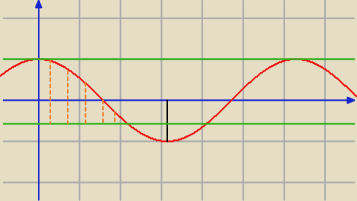 y = cos(x)
y = cos(x)
17 wrz 18:47
ZKS:
Przepraszam Aga1 nie odświeżałem i nie zobaczyłem Twojego wpisu.
17 wrz 18:48
