PANIE BOGDANIE Damian: Czy przykład ten co napisałem może służyć jako dowód że ten wzór skróconego mnożenia jest liczbą NIEUJEMNĄ Chce udowodnić że (a−b)² ≥0 ZAWSZE wiec: (x−a)² < 0 x² − 2ax + a² < 0 Δ= 4a² − 4a² = 0 Δ=0 wiec istnieje x₀

	−b		2a
x0 = </div>		=		= 1
	2a		2a

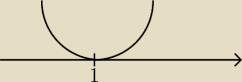
Czyli wykres niżej...

Damian:

Damian: JAko że cenię sobie porady innych to zapraszam do skomentowania mojej propozycji...

pomocy!!: jest kwadrat to bedzie zawsze +

Damian: tak to wiem ale trzeba to udowadniac w inny sposób

pazio: mi się wydaje, że nie, ale jak tak patrzę no to, co tam jest napisane, to sobie myślę, że może ja po prostu głupia z tej matmy jestem...? no bo kwadrat jakiejś liczby ZAWSZE będzie nieujemny i mi się wydawało, że to starczy takie stwierdzenie...

pomocy!!: mi tez

♊: Twoje rozwiązanie jest jak najbardziej poprawne Ja bym rozpatrzył 3 przypadki: 1. a=b _{(albo a−b =0)} 2. a>b _{(albo a−b >0)} 3. a<b _{(albo a−b <0)} 1. (a−b)²=0²=0 2. a>b ⇒ a−b = c, c>0 c² >0 3. a<b ⇒ a−b = −c, −c<0 (−c)² = (−c)(−c) = c*c = c² >0 Albo wykorzystał własność, że |a| = √a² (a−b)²≥0 / √( ) pierwiastkuję obustronnie − to nie zmienia znaku √(a−b)²≥√0 |a−b|≥0

♊: pazio & pomocy!!: najpierw trzeba coś udowodnić (a własciwie umieć udowodnić) żeby to stosować. Oczywiście, można po prostu ufać nauczycielom, ale później (studia czy cośtam) będzie trzeba umieć takie rzeczy udowadniać ;) Z tym wykorzystaniem wartości bezwzględnej to chyba nei można z tego kskorzystac udowadniając to, bo wtedy zakładam, że (a−b)² ≥ 0, a nie mam zakładać tylko dowieść :)

Damian: OOOO twoje pierwsze dowodzenie jest spoko a wart. bezwzględna odpada bo w dowodzeniu sie jej nie stosuje... Zgadzam się z tobą że czasem trzeba coś udowodnić A że jest to czas studiów to fajnie sie pobawić w udowadnianie twierdzeń... a innym wydaje sie ze nie trzeba... bo po co... fajnie sie cos stosuje jak w przyszłości dostane taki przypadek to tak właśnie będę udowadniał jak ty na kolorowo dzieki

♊: Ale wiesz − nie zawsze znajdziesz kolorowe długopisy jak będziesz coś udowadniał ;P Taki żarcik z tymi kolorami

Damian: spoko ale przynajmniej wiadomo co do czego i łatwo znaleść

Bogdan: Damianie, przepraszam, ze nie odpowiedziałem od razu, ale miałem inne zajęcia. Cytuję to, co napisałeś (w nawiasach { } umieszczam komentarz): Chcę udowodnić że (a−b)² ≥0 ZAWSZE więc: (x−a)2 < 0 {stosujesz jak widzę dowód nie wprost, należało napisać: zakładam, że (x − a)² < 0} x² − 2ax + a² < 0 {niepotrzebnie, bo jeśli rozwijasz (x − a)² wzorem skróconego mnożenia do postaci trójmianu kwadratowego, to oczywistością jest, że Δ = 0} Δ= 4a² − 4a² = 0 Δ=0 wiec istnieje x₀ {to x_o = a, co można było zauważyć bez liczenia Δ}

	−b
x0 =		{pewna niekonsekwencja, w trójmianie x2 − 2ax + a2 występuje
	2a

oznaczenie a, nie można więc użyć tej litery do opisania innej wielkości występującej w tym trójmianie, poprawnie

	−B
byłoby np. tak: x0 =		, gdzie A = 1, B = −2a}
	2A

	−b		2a
x0 =		=		{poważny błąd, skąd w mianowniku wzięło się a, powinno
	2a		2a

	−b		2a
być x0 =		=		= a, a jeszcze poprawniej byłoby tak:
	2a		2

	−B		2a
x0 =		=		= a}
	2A		2

czyli wykres niżej {rysunek przedstawia szkic wykresu funkcji kwadratowej, która przyjmuje wartości ≥ 0, nigdzie nie jest ujemna, co należało zamknąć stwierdzeniem, że założenie (x−a)2 < 0 jest fałszywe, a więc (x−a)2 ≥ 0 dla każdej wartości x∊R}

b.: Jednak łatwiej dowodzić tak, jak proponowała Pazio: rozważmy dwa przypadki: 1. a−b≥0. Wówczas (a−b)²≥0, bo iloczyn dwóch liczb nieujemnych jest nieujemny. 2. a−b<0 Wówczas (a−b)²=(a−b)*(a−b)=(−1)*(−1)*(b−a)*(b−a) = (b−a)²>0, bo iloczyn dwóch liczb dodatnich (b−a>0) jest dodatni. (Albo od razu: iloczyn dwóch liczb ujemnych jest dodatni).