pomocy maja:): W urnie znajduje się pięć kul białych i cztery czarne. Losujemy kolejno bez zwrotu dwie kule. Oblicz za pomocą drzewa stochastycznego prawdopodobieństwo wylosowania kul tego samego koloru

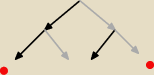
Patronus: pierwszy wybór:

	1
Prawd. wylosowania kuli białej =
	5

	1
Prawd. wylosowania kuli czarnej =
	4

drugi wybór

	1
Jeśli I była czarna to druga czarna to
	3

	1
Jeśli I była biała to druga biała to
	4

Czyli prawd. wylosowania dwóch kul tego samego koloru to:

	1		1		1		1		1		1		3 + 5		2
P(A) =		*		+		*		=		+		=		=
	5		4		4		3		20		12		60		15

ICSP: Patronus a to nie będzie przypadkiem :

	5		4
Prawd. wylosowania kuli białej =		a czarnej		w pierwszym wyborze ?
	9		9

Patronus: taaa, będzie − to całe drzewo zawsze mi zaburza myślenie Przepraszam, całe obliczenia są źle.

ICSP: krzakoterapia

PW: ICSP, masz rację. Drzewka to ogłupianie narodu. Zadanie jest proste: Zdarzeniami elementarnymi są dwuelementowe podzbiory zbioru 9−elementowego. Zdarzenia sprzyjające to takie, w których te dwuelementowe podzbiory są brane ze zbioru 5−elementowego (białe) lub z rozłącznego z nim zbioru 4−elementowego (czarne). Odpowiedź: Wszystkie zdarzenia elementarne są jednakowo prawdopodobne (wynika to z treści zadania − ze sposobu losowania), a więc na mocy twierdzenia zwanego klasyczną definicją prawdopodobieństwa ... Co miałoby ilustrować w tym wypadku drzewko, zwane szumnie (żeby było śmieszniej) drzewkiem stochastycznym? Ani zdarzeń elementarnych w tym drzewku nie widać, ani prawdopodobieństw jednakowych.