Całka oznaczona Tiamat: Sporządź rysunek i oblicz pole obszaru ograniczonego liniami: y=x² x=y² Proszę baaaaardzo o rozwiązanie bo nie wiem kompletnie jak robić te całki, skąd brać całke w ogóle itd, będę wdzięczna za konkretną pomoc: )

AS: 1. Naszkicować wykresy obu funkcji w jednym układzie współrzędnych 2. Ustalić granice całkowania rozwiązując układ równań {y = x² , x = y²} 3.Obliczyć pole wzorem P = ∫(G(x) − D(x))dx gdzie G(x) równanie krzywej wyżej położonej , D(x) równanie krzywej niżej położonej.

Tiamat: Właśnie mam problem z tymi granicami, zrobiłam coś takiego: √x = x² l .x² x= x⁴ l −x 0 = x⁴ − x Δ=1 x₁ = 0 x₂ = 1 Czyli granicami jest 0 i 1 ? Generalnie ostatecznie wyszło mi ¹₃

AS: Dopisek: Wynik końcowy: P = 1/3

Tiamat: Czyli to dobry sposób na znalezienie granic? Może ona wyjść ujemna?

AS: Obliczenia poprawne − gratulacje.

AS: Rozwiązanie układu równań bardzo problematyczne. y = x² i y = √x => √x = x² => x = x⁴ => x(x³ − 1) = 0 => x = 0 lub x = 1 Zakres całkowania <0,1>

ania: Jak można liczyć deltę z równania w 4 potędze ;>

Tiamat: podstawiłam x² = t ale to była totalna prowizorka: D t² − x = 0 o takim rozwiązaniu nie pomyślałam: )

Tiamat: No dobrze, mam jeszcze pytanie co zrobić jeśli mam jeszcze bardziej namotane: 2x³ = √4x l .x² w skrócie: x(4x⁴ − 4) = 0 czyli x=0 x=1 tak?: )

Basia: poprzedni układ powinien być rozwiązany tak: y = x² y² = x (x²)² = x x⁴ = x x⁴ − x = 0 x(x³−1)=0 x=0 ∨ x³−1=0 ⇔ x=0 ∨ x=1 a tutaj też pewnie coś namotałeś z tym pierwiastkiem, więc podaj oryginalne wzory funkcji

Tiamat: Oryginalnie jest tak: y=2x³ i y² = 4x

Basia: (2x³)² = 4x 4x⁶ − 4x = 0 4x(x⁵−1) = 0 x=0 ∨ x⁵−1=0 x=0 ∨ x⁵=1 x=0 ∨ x=1

Tiamat: Ok, wyszło mi tak chociaż robiłam inaczej, ale dzięki wielkie już mniej więcej wiem jak to zrobić: )

Basia: ten zapis y=√4x = 2√x nie jest błędny, ale niepotrzebnie utrudnia obliczenia

Tiamat: okk a całka z tego w takim razie ma wyglądać tak: ∫2x³ − √4x dx czy ∫4x⁶ − 4x dx ? Czy może to obojętne?: )

Basia: ale też i nie do końca poprawny jak już chcesz pierwiastkować to masz y² = 4x ⇔ y = √4x ∨ y = −√4x i musisz rozwiązywać dwa układy równań

Basia: nie jest obojętne ponieważ x∊<0;1> (bo to będą granice całkowania) obszar wyznaczają: y = 2x³ i y=√4x=2√x (układ y=2x³ i y=−√4x nie ma rozwiązania) czyli P = ₀∫¹[ 2√x − 2x³ ] dx

Tiamat: Nawet jeśli wg wykresów ta część która mnie interesuje jest ponad osią x i po prawej oy?:3

Tiamat: Chodzi mi o samą postać całki

Basia: źle napisałam: układ: y = 2x³ y = −2√x ma tylko jedno rozwiązanie x=0 i żaden obszar tam nie powstaje reszta w porządku

Basia: już napisałam: P = ₀∫¹ [ 2√x − 2x³ ] dx naszkicuj wykresy: wykres y = 2√x "jest wyżej" niż wykres y = 2x³

Basia: oczywiście w przedziale [0;1]; potem jest odwrotnie

Basia: 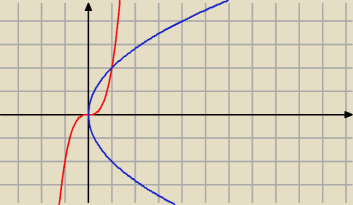y=2x³ y²=4x

Tiamat: Ok, faktycznie jest wyżej... Hmm przeliczę to ładnie i napiszę odpowiedź i zobaczymy czy już mi wyjdzie: )

Tiamat: ∫ 2 √x − 2x³ dx = 2∫ x^1/2 dx − [ ¹₄ 4x⁴ ] = [ ⁴₃x^3/2 − ¹₂x⁴ ]

Tiamat: podstwiając:

4		1		8		3		5
	. 1 −		=		−		=
3		2		6		6		6

Basia: masz tam błąd w zapisie, ale to chyba literówka bo potem jest dobrze ∫[2√x−2x³]dx = 2[∫√xdx − ∫x³dx] =

	x3/2		x4
2(		−		) =
	32		4

4		1
	*x3/2 −		x4
3		2

P dobrze

Tiamat: Ok, super dzięki wielkie za pomoc, mam jeszcze 20 takich zadań i egzamin za tydzień: D

Tiamat: No dobrze kolejna wątpliwość: y=x³ i y=4x 4x= x³ 0 = x³ − 4x 0 = x(x² − 4) x=0 Δ = 16 √Δ = 4 x₁ = −2 x₂ = 2 I tu pojawił się problem posiadania aż trzech granic co jest dość problematyczne, ale logiczne, zatem wybrałam x₂ = 2 ponieważ potem pomnożę całkę razy 2 (to −2 jest granicą tego samego pola ale po drugiej stronie osi − tak myślę przynajmniej) Tylko, że pole wyszło mi ujemne (o.0) i pytanie która właściwie funkcja jest tą u "góry"? Wychodzi na to, że to x³ powinno być na górze i wtedy wyjdzie mi pole = 2 Pytanie: Czy to jest w ogóle dobrze? Z góry dziękuję dobrym ludziom, którzy pomogą mi w ty: )

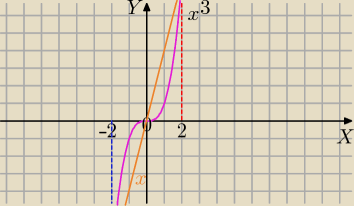
Mila: Funkcja y=x³ jest nieparzysta, masz dwa obszary. P=2₀∫²(4x−x³)dx= {P=8}

Tiamat: Okk, tak mi wyszło: ) I żeby nie zakładać tysiąca tematów wrzucę tu jeszcze jedno problematyczne zadanie dotyczące tego tematu:

	π
y=		y = arctgx x=0
	3

Wykres narysowałam, no i zacięłam się na:

π
	= arctgx
3

Nie wiem czy mam szukać jakiś tabel z wartościami f. trygonometrycznych/kołowych, czy jakoś (jak?) to ciągnąć dalej? :c

Mila:

π
	=arctgx / obustronnie tg
3

	π
tg		=x
	3

x=√3

Tiamat: Czyli w zasadzie można to znaleść w tablicach, jeśli się je ma pod łapą. √3

	π
∫		− arctgx dx
	3

0

Tiamat: Co zrobić z taką całką? :C