zadanie z dowodem
demo:

Witam
"Korzystając z definicji funkcji malejącej wykaż, że funkcja f(x) = |x+2| jest malejąca w
zbiorze (−
∞; −2>"
oczywiście założenia:
D
f = R
x
1 ⋀ x
2 ∊ (−
∞; −2>
x
1 > x
2
teza:
f(x
1) > f(x
2)
f(x
2) − f(x
1) < 0
dowód:
|x
2+2| − |x
1+2| < 0
x
2 = −2 ⋁ x
1 = −2
|x
2+2| = {x
2+2; x
2+2 ≥ 0
{−x
2−2; x
2+2 < 0
|x
1+2| = {x
1+2; x
1+2 ≥ 0
{−x
1−2; x
1+2 < 0
{x ∊ (−
∞; −2>
{−x
2 −2 + x
1+2 < 0
x
1 − x
2 < 0
Gdzie jest błąd? coś mi się wydaje że wszystko jest źle ;x
proszę o pomoc
16 wrz 15:53
Ajtek:
Błędnie postawiona teza funkcji malejącej.
16 wrz 16:02
demo: @Ajtek
f(x1) − f(x2) > 0
f(x1) − f(x2) = |x1+2| − |x2+2| = −x1 − 2 + x 2 + 2 = −(x1 − x2)
uzasadnienie:
x1 − x2 > 0
−(x1 − x2) < 0
czyli dalej coś nie gra... :c
16 wrz 16:13
sushi_gg6397228:
x1>x2 to f(x1) <f(x2) to dla malejacej
x1>x2 to f(x1) > f(x2) to dla rosnacej
16 wrz 16:25
sushi_gg6397228:
oraz dowod zaczyna sie od "iksów" a nie "f(x)"
16 wrz 16:29
demo: aha... nie rozumiem dlaczego f(x1) <f(x2) ale mniejsza o to.
wyliczenia w takim razie mam dobre? złe?
16 wrz 16:30
Ajtek:
Jeżeli błędnie postawiona teza to i wyliczenia złe!
16 wrz 16:32
Ajtek:
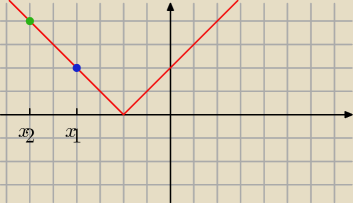
A dlaczego f(x
1)<f(x
2)

masz założenie x
1>x
2 i teraz patrz na rysunek.
Niebieska kropka f(x
1), zielona f(x
2), już widzisz dlaczego

16 wrz 16:36
demo: aha. dzięki! teraz rozumiem (nie mam wyobraźni przestrzennej

)
sprawdź teraz:
teza:
f(x
1) < f(x
2)
dowód:
x
1 > x
2 ⇔ x
1 − x
2 >0
f(x
1) < f(x
2) ⇔ f(x
1) − f(x
2) < 0
|x
1+2| − |x
2+2| = −x
1 − 2 + x
2 + 2 = − x
1 + x
2 = − (x
1−x
2)
uzasadnienie:
x
1−x
2 > 0 − założeń
− (x
1−x
2) − ? kurde nie wiem już. pogubiłem się...
16 wrz 19:39
demo: up
16 wrz 21:04
demo: up
16 wrz 21:04
 Witam
"Korzystając z definicji funkcji malejącej wykaż, że funkcja f(x) = |x+2| jest malejąca w
zbiorze (−∞; −2>"
oczywiście założenia:
Df = R
x1 ⋀ x2 ∊ (−∞; −2>
x1 > x2
teza:
f(x1) > f(x2)
f(x2) − f(x1) < 0
dowód:
|x2+2| − |x1+2| < 0
x2 = −2 ⋁ x1 = −2
|x2+2| = {x2+2; x2+2 ≥ 0
{−x2−2; x2+2 < 0
|x1+2| = {x1+2; x1+2 ≥ 0
{−x1−2; x1+2 < 0
{x ∊ (−∞; −2>
{−x2 −2 + x1+2 < 0
x1 − x2 < 0
Gdzie jest błąd? coś mi się wydaje że wszystko jest źle ;x
proszę o pomoc
Witam
"Korzystając z definicji funkcji malejącej wykaż, że funkcja f(x) = |x+2| jest malejąca w
zbiorze (−∞; −2>"
oczywiście założenia:
Df = R
x1 ⋀ x2 ∊ (−∞; −2>
x1 > x2
teza:
f(x1) > f(x2)
f(x2) − f(x1) < 0
dowód:
|x2+2| − |x1+2| < 0
x2 = −2 ⋁ x1 = −2
|x2+2| = {x2+2; x2+2 ≥ 0
{−x2−2; x2+2 < 0
|x1+2| = {x1+2; x1+2 ≥ 0
{−x1−2; x1+2 < 0
{x ∊ (−∞; −2>
{−x2 −2 + x1+2 < 0
x1 − x2 < 0
Gdzie jest błąd? coś mi się wydaje że wszystko jest źle ;x
proszę o pomoc
 A dlaczego f(x1)<f(x2)
A dlaczego f(x1)<f(x2) masz założenie x1>x2 i teraz patrz na rysunek.
Niebieska kropka f(x1), zielona f(x2), już widzisz dlaczego
masz założenie x1>x2 i teraz patrz na rysunek.
Niebieska kropka f(x1), zielona f(x2), już widzisz dlaczego
 )
sprawdź teraz:
teza:
f(x1) < f(x2)
dowód:
x1 > x2 ⇔ x1 − x2 >0
f(x1) < f(x2) ⇔ f(x1) − f(x2) < 0
|x1+2| − |x2+2| = −x1 − 2 + x2 + 2 = − x1 + x2 = − (x1−x2)
uzasadnienie:
x1−x2 > 0 − założeń
− (x1−x2) − ? kurde nie wiem już. pogubiłem się...
)
sprawdź teraz:
teza:
f(x1) < f(x2)
dowód:
x1 > x2 ⇔ x1 − x2 >0
f(x1) < f(x2) ⇔ f(x1) − f(x2) < 0
|x1+2| − |x2+2| = −x1 − 2 + x2 + 2 = − x1 + x2 = − (x1−x2)
uzasadnienie:
x1−x2 > 0 − założeń
− (x1−x2) − ? kurde nie wiem już. pogubiłem się...