Z koła o średnicy 8 cm wycięto trójkąt równoboczny potrzebujacy: Z koła o średnicy 8 cm wycięto trójkąt równoboczny wpisany w to koło. Oblicz pole pozostałej części koła.

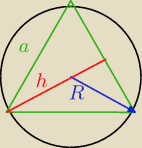
dero2005: R = 4 ²₃h = R ⇒ h = a = ²₃√3h

	a2√3
Pt =
	4

P_k = πR² P_k − P_t =

potrzebujacy: nie wiem jak mam to dalej obliczyc ile wynosi ta ¹₃ h albo jak wyglada dokonczone zadanie

Bogdan:

	1		2
Warto skorzystać z zależności: R =		a√3 zamiast z R =		h.
	3		3

	2
To jakaś niedobra maniera upierania się w takich sytuacjach z R =		h, co wymaga
	3

wprowadzenia kolejnej zmiennej h.

	1
R =		a√3 /*√3 ⇒ a = R√3 ⇒ a2 = 3R
	3

	1		1
Pole trójkąta P =		a2√3 =		*3R√3
	4		4

W tym zadaniu: R = 4 ⇒ a² = 3*4 = 12

dero2005: ²₃h = R |*3 2h = 3R :2 h = ³₂R = 6 a = ²₃√3*h = ²₃√3*6 = 4√3

	a2√3		(4√3)2*√3
Pt =		=		= 12√3
	4		4

P_k = πR² = π*4² = 16π P_k − P_t = 16π−12√3 = 4(4π−3√3) ≈ 29,49 cm²