Twierdzenie o środkowych trójkąta Ala: W trójkącie ABC, gdzie |AC|=|BC|=√10, środkowe poprowadzone z wierzchołków A oraz B przecinają się pod kątem 90°. Znajdź długość podstawy tego trójkąta. Proszę o pomoc w rozwiązaniu zadania

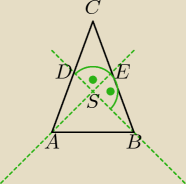
loitzl9006: Skorzystaj z tego, że środkowa dzieli bok na dwa równe odcinki, np. |CE| = |BE| i że punkt przecięcia środkowych w każdym trójkącie dzieli odcinki środkowych w relacji 2:1 Czyli inaczej |AS| = 2|SE| i |SB| = 2|DS| Ponieważ |BE| jest połową |BC| i znasz związek pomiędzy |SE| i |SB|, to możesz napisać twierdzenie Pitagorasa dla trójkąta SEB i powstanie w ten sposób równanie z jedną niewiadomą |SB|. Jak ją wyliczysz, to potem z trójkąta równoramiennego prostokątnego ABS wyliczysz długość podstawy AB.

pigor: .. a więc z podziału środkowych w stosunku 2k : k masz z ΔABS bok AB np. jako przekątną kwadratu o boku 2k, czyli (*) |AB|=2k√2= ?, przy czym z ΔBSE : k²+(2k)²=(¹₂√10)² ⇔ 5k²=¹₄*10 ⇒ k= ¹₂√2 , więc z (*) : |AB|=2*¹₂√2*√2= 2 − szukana długość podstawy Δ . ...