Pole powierzchni bocznej ostrosłupa
Morgan: Oblicz pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego o krawędzi bocznej b i
kącie nachylenia ściany bocznej do płaszczyzny podstawy alfa.
15 wrz 17:03
gość:
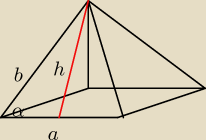
wyliczamy h i a
h=b*sinα
a=2b*cosα
| | 1 | | 1 | |
pole jednego trójkąta P= |
| ah= |
| *2bcosα*bsinα=b2*sinα*cosα |
| | 2 | | 2 | |
P
Pb=4b
2*sinα*cosα
15 wrz 17:27
Morgan: kąt alfa to kąt nachylenia ściany bocznej do krawędzi podstawy, a nie tak jak zaznaczyłeś/aś
kąt między krawędzią ściany bocznej do krawędzi podstawy.
15 wrz 17:30
gość: | | a*√2 | |
narysuj to sobie i wylicz z sinusa H a z cosinusa a ( trójkąt o bokach H, |
| ,b) |
| | 2 | |
15 wrz 17:48
Morgan: | | 4b2 tgα | |
Mnie wyszło : |
| Pole boczne= 4 * r *h |
| | (2+ tg2α) sinα | |
H− równe tgα *r
r obliczyłam z pitagorasa podstawiając b
2= H
2 + (r
√2)
2
15 wrz 17:53
dero2005:
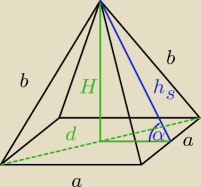
15 wrz 18:00
Morgan: Tak też właśnie sobie rozrysowałam, dodatkowo że a=2r może wprowadza troche zamętu no ale tak
podstawiłam
15 wrz 18:06
dero2005:
| a | | a | |
| = cosα ⇒ hs = |
|
|
| 2hs | | 2cosα | |
a = 2h
s*cosα
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| | 2bcosα | | b | | 4b2cosα | |
Pb = 2a*hs = 2* |
| * |
| = |
| |
| | √1+cos2α | | √1+cos2α | | 1+cos2α | |
15 wrz 18:08
Morgan: dero2005 bardzo dziękuję

trochę za dużo wprowadziłam tych oznaczeń i pogubiłam po
drodze, jeszcze raz dziękuję
15 wrz 18:40


 trochę za dużo wprowadziłam tych oznaczeń i pogubiłam po
drodze, jeszcze raz dziękuję
trochę za dużo wprowadziłam tych oznaczeń i pogubiłam po
drodze, jeszcze raz dziękuję