rozłóż na czynniki kasia: czesc, może mi ktoś pomoc rozłożyć na czynniki ? x⁷−x⁵+1

Basia: nie pomyliłaś się ? ten wielomian nie ma pierwiastków wymiernych nie jest łatwo go rozłożyć

kasia: nie, nie pomysliłam się..

kasia: halo ?

PW: Trudne. Na razie wymyśliłem, że miejsce zerowe jest jedno (między −1 a 0). Mówię o rozwiązaniu w R. Doszedłem do tego metodą badania funkcji, a więc "niealgebraicznie" i dalej nie wiem. Można popaść w stan uzależnienia przy takich zadaniach. Może ktoś mądrzejszy?

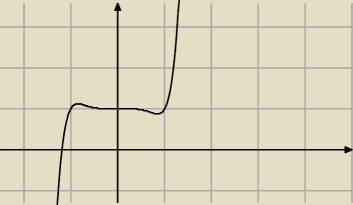
Patronus: Z tego wykresy wynika, że pierwiastek jest odrobinę mniejszy od −1

Piotr: trzeba poczekac na ICSP

PW: Jasne, też wyliczyłem, że ciut mniejszy i potem przestawiło mi się w momencie pisania.

	5		5
Jest f(−1) = 1, a już f(−		) < 0, a więc miejsce zerowe jest między −		a 1.
	4		4

Wielomian jest więc iloczynem funkcji liniowej i trzech nierozkładalnych funkcji kwadratowych, ale standardowe metody podstawiania zawodzą. Na pewno nie wpadniemy na pomysł, co dodać i odjąć, żeby powyłączać wspólne czynniki.

kokosy: http://www.wolframalpha.com/input/?i=x^7-x^5%2B1%3D0 −1,19 niezly wielomian

Artur_z_miasta_Neptuna: Tego wielomianu nie da się rozłożyć na czynniki. Można tylko podać przybliżone wartości tychże pierwiastków i nic ponad to. To zadanie jest 'jak znalazł' na metody numeryczne. Prosty programik w C++ i są wyniki (pierwiastki)

ICSP: bisekcja moim zdaniem

Trivial: Tak sobie pomyślałem, że jeszcze nigdy metody bisekcji nie zaimplementowałem. Oto więc prosty programik w Haskellu: bisection :: (Ord a, Floating a) => (a -> a) -> a -> a -> a bisection f a b | abs (a-b) < dx = a | (f a)*(f m) < 0 = bisection f a m | otherwise = bisection f m b where m = (a+b)/2 dx = 0.000000001 main = print $ bisection (\x -> x^7 - x^5 + 1) (-3) 0

wsl: http://forum.zadania.info/viewtopic.php?f=32&t=40602&p=149421#p149421

ICSP: tam jest + przed x⁵ a tutaj mamy −