całki wojti: 1. Jak policzyć ∫1/(x²−x) dx od 2 do∞ 2. ∫∫cos(2x²+2y² +5) dxdy po zbiorze D: x²+y²≤4 ; x≥0 i y≥0 3. ∫∫∫yz dxdyd po zbiorze Ω: √9−x²−y² ; z=0 i y>0

Vizer: 1. Ułamki proste myślę, ze poskutkują no i potem mamy całkę niewłaściwą to liczymy granicę, chyba wiadomo co i jak 2. i 3. to zadania, które trzeba sobie narysować W 2. mamy koło o promieniu równym 4 i środku w punkcie (0,0) i wiemy, że interesuje nas pierwsza ćwiartka układu, wiec ćwierć koła. Przejść będzie chyba trzeba na współrzędne biegunowe dla ułatwienia obliczeń. W 3. Mamy pół sferę, albo kulę, nie ma tak żadnej równości czy nierówności, ciężko więc stwierdzić i kolejne warunki należy zastosować.

wojti: a w drugim nie jest to koło o promieniu 2?

Vizer: Racja straszelna pomyłka, za którą serdecznie przepraszam

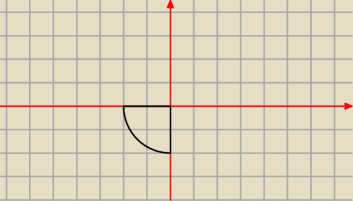
wojti: to 2 będzie wyglądało następująco: całkujemy funkcję cos(2x²+2y²+5) w obszarze widocznym na rysunku. (ćwiartka koła od pi do 3/2pi) we współrzędnych biegunowych będziemy mieli funkcję cos(2r²cos²φ+2r²sin²φ+5) co daje cos(2r²+5) całkujemy w granicach π≤φ≤3/2π i 0≤r≤2 ∫∫cos(2r²+5)rdrdφ=∫(sin(2r²+5)/4dφ od 0 do 2= ∫(sin(13)−sin(5))/4dφ=(−cos(13)φ+cos(5)φ)/4 od π do 3/2π = (−3πcos(13)+3πcos(5))/8−(−2πcos(13)+2πcos(5))/8=(−πcos(13)+πcos(5))/8 dobrze rozumiałem czy gdzieś robię błąd?

Krzysiek: x≥0,y≥0 czyli φ∊[0,π/2] −pierwsza ćwiartka a nie trzecia

wojti: faktycznie. to końcówka zmieni się na: (−cos(13)φ+cos(5)φ)/4 od 0 do π/2 = (−πcos(13)+πcos(5))/4 i to będzie ostateczny wynik.

Krzysiek: w Twoim poście o 19.08 nie rozumiem jak zachodzi 3 równość... skąd Tobie się bierze cos z sin? Tego nie całkujesz bo to jest stała...

	π
więc ostateczny wynik to: (sin(13)−sin(5))/4 *
	2

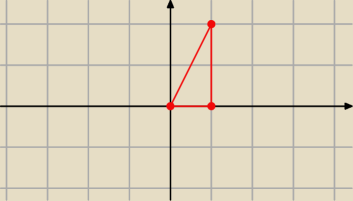
wojti: dzięki wielkie przegapiłem to. Jeżeli muszę policzyć objętość bryły która ma w podstawie trójkąt jak na rysunku A(0,0,0) B(1,0,0) i C(1,2,0) i została ścięta powierzchnią z=6−x²−y² to będzie całka podwójna ∫∫6−x²−y²dydx 0≤x≤1 i 0≤y≤2 czy w y wpisuję od 0 do 2x?

Krzysiek: dla 0≤x≤1 i 0≤y≤2 obszarem jest prostokąt więc źle. powinno być 0≤y≤2x czyli Twoja druga opcja

wojti: dzięki

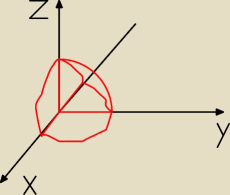
wojti: z=√9−x²−y² z=0 i y>0 muszę policzyć ∫∫∫yzdxdydz po tym zbiorze. jest to jedna czwarta okręgu jak na rysunku. wiem że trzeba zmienić na wsp sferyczne tylko nie wiem jakie będą granice. Po przejściu będzie ∫∫∫(rcosθsinΦ rsinθ)(−r²cosθ)drdΦdθ r powinno być w granicach 0≤r≤3 θ wydaje mi się że 0≤θ≤π/2 i wtedy Φ w −π/2≤Φ≤π/2 dobrze myślę czy znowu gdzieś robię błąd?

Krzysiek: jak dla mnie to jest: Jakobian: r² cosθ Φ∊[0,π] (I i II ćwiartka) θ ∊[0,π/2] ( z>0)

wojti: ok zamieniłem x z y i stąd mi wyszło −π/2≤Φ≤π/2 jakobian zawsze jest r²cosθ?

Krzysiek: http://pl.wikipedia.org/wiki/Uk%C5%82ad_wsp%C3%B3%C5%82rz%C4%99dnych_sferycznych widziałem, że użyłeś systemu "geograficznego" więc wtedy tyle wychodzi