ostrosłupy slaby z matmy: Jakie pole powierzchni ma ostrosłup prawidłowy trójkątny o wysokości 5 cm i krawędzi podstawy 9cm

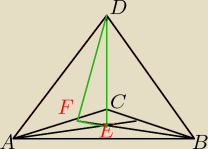
ag: BF − wysokość trójkąta równobocznego o boku długości 9

	a√3
h=
	2

	9√3
h=
	2

	1
|EF|=		h
	3

	1		9√3		3√3
|EF|=		*		=
	3		2		2

|ED|=5 z twierdzenia Pitagorasa |EF|²+|ED|²=|FD|²

	3√3		9*3		27		100		27		127
|FD|2=52 + (		)2 = 25 +		= 25 +		=		+		=
	2		4		4		4		4		4

	√127
|FD|=
	2

pole ściany bocznej

	1		√127		9√127
P=		*9*		=
	2		2		4

	9√127		27√127
PPb = 3*		=
	4		4

	a2√3		81√3
Pp=		=
	4		4

	27√127		81√3
PC=		+
	4		4

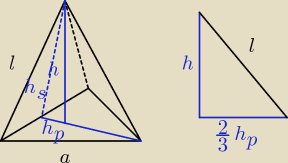dero2005: a = 9 h = 5

	a√3		9
hp =		=		√3 → wysokość podstawy
	2		2

l² = (²₃h_p)² + h² l = 2√13 → długość krawędzi bocznej h_s² = l² − (^a₂)²

	√19
hs =		→ wysokość ściany bocznej
	2

	a2√3		81
Pp =		=		√3 → pole podstawy
	4		4

	a*hs		27
Pb = 3*		=		√19 → pole boczne
	2		4

	27
Pc = Pp + Pb =		(3√3+√19) → pole całkowite
	4

dero2005: wprowadzam poprawkę w obliczeniach gdyż zakradł się bląd

	√127
hs =
	2

	27
Pb =		√127
	4

	27
Pc =		(3√3+√127)
	4

vgi: w graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość 12, a wysokość wynosi 8. jakie pole ma przekrój zawierający wysokość podstawy i krawędź boczną?