wartosc bezwzgledna
mcjng: |f(x)|=x2−4 to rysuję tylko tą częśc ramion od osi OX w górę tak?
14 wrz 16:18
wmboczek: Te zostają, a część pod osią odbijasz symetrycznie nad oś
14 wrz 16:53
mcjng: | | f(x)+1 | |
|x|= |
| a jak to się robi? |
| | 2−f(x) | |
14 wrz 17:32
Jakub: Nie wydaje mi się
wmboczek, że dobrze napisałeś. Przykładowo, do Twojego wykresu należy
punkt (1,3). Podstawiam, do równania współrzędne tego punktu
|f(1)| = 1
2 − 4
|f(1)| = −3
Równość fałszywa, więc punkt (1,3) nie powinien należeć do wykresu funkcji, której wzór spełnia
równania |f(x)| = x
2−4.
To co napisałeś, odnosi się do funkcji f(x) = |x
2−4|.
mcjng napisał dobrze, rysuje f(x) = x
2−4 opuszczając część wykresu pod osią Ox.
@
mcjng
Wyznacz wzór funkcji f(x)
|x|(2−f(x)) = f(x) + 1
2|x| − |x|f(x) = f(x) + 1
2|x| − 1 = f(x) + |x|f(x)
2|x| − 1 = f(x)(1+|x|)
| | f(x)+1 | |
Ustal dziedzinę na podstawie |x| = |
| tzn. f(x) ≠ 2 (mianownik różny od zera) |
| | 2−f(x) | |
Następnie narysuj część wykresu dla x ≥ 0 i x < 0.
14 wrz 18:31
mcjng:
Mi generalnie chodzi o to, że nie wiem jak z takim zapisem właśnie postąpić. Bo od tej
| | f(x)+1 | |
ostatniej wersji którą napisałeś, to ja właśnie wyszedłem do mojego |x| = |
| . |
| | 2−f(x) | |
Teraz myślałem, że skoro |x|≥0 czyli wartosc bezwzgledna przyjmuje wartosci nieujemne, to może:
14 wrz 19:03
mcjng: podbijam
14 wrz 22:05
Artur_z_miasta_Neptuna:
wmboczek
z zapisu |f(x)| oznacza, że zbiór wartości funkcji musi być większy od zera ... dlatego w
pierwszym zadaniu rysuje się TYLKO ramiona ≥0
zał. f(x)≠2
| f + 1 | | −1−f | | 2−f−3 | | −3 | | 3 | |
| = − |
| = − |
| = −1 − |
| = −1 + |
| |
| 2−f | | 2−f | | 2−f | | 2−f | | 2−f | |
a więc:
wyjściowe równianie przekształcasz w:
i rysujesz
14 wrz 22:12
Artur_z_miasta_Neptuna:
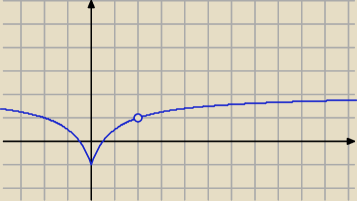
14 wrz 22:13
Artur_z_miasta_Neptuna:
tfu .... źle ... bez wyrzucenia ów punktu
14 wrz 22:13
Artur_z_miasta_Neptuna:
| | 2|x|−1 | |
a skoro wychodziłeś od f(x) = |
| ... to przecież: |
| | |x|+1 | |
| | 2|x|+2 − 3 | | 3 | |
f(x) = |
| = 2− |
| ... i coś takiego (jak widzisz) łatwo naszkicować |
| | |x|+1 | | |x|+1 | |
14 wrz 22:17
Eta:
| | 2|x|−1 | | 1 | |
f(x)= |
| = 2− |
| |
| | |x|+1 | | |x|+1 | |
| | 1 | |
dla x≥0 f(x)= 2− |
| −−− narysuj t te gałęzie hiperboli dla x≥0 |
| | x+1 | |
i
| | 1 | | 1 | |
dla x<0 f(x)= 2− |
| = 2+ |
| |
| | −x+1 | | x−1 | |
14 wrz 22:21
Eta:
Echh chochlik zamiast 1 ma być
3 
14 wrz 22:23
Mila:
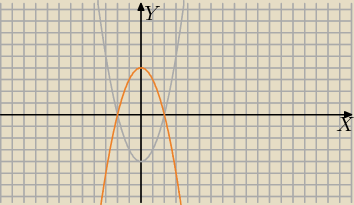
1) wykres:
|f(x)|=x
2−4
|y|=x
2−4
|y|=y dla y≥0⇔y=x
2−4 (wykres tylko nad osią OX)
|y|=−y dla y<0
−y=x
2−4
y=−x
2+4 ( wykres tylko pod osią OX)
Nie umiem narysować − w każdym bądź razie odrzucasz wykresy dla x∊(−2;2) (te z wierzchołkami)
14 wrz 22:34
Mila: Zadanie 2 Eta napisała, czy coś jeszcze wyjaśnić?
14 wrz 22:42
Mila: Witaj Eto! Czy może Tobie uda się rysunek z zadania 1.(bez tego "środka")
14 wrz 22:43
mcjng:
[f(x)+1][2−f(x)]≥0
dobrze?
15 wrz 09:56
Basia:
nie; nie możesz mnożyć przez 2−f(x) bo nie wiesz czy to wyrażenie jest dodatnie
| L | |
| ≥ 0 ⇔ [ L≥ 0 ∧ M>0 ] ∨ [ L≤0 ∧ M<0 ] |
| M | |
15 wrz 11:53
Basia:
oj sorry; oczywiście dobrze; jednak jeszcze śpię
ale
ściśle powinno być tak:
| f(x)+1 | |
| ≥ 0 ⇔ [f(x)+1]*[2−f(x)] ≥ 0 ∧ 2−f(x)≠0 |
| 2−f(x) | |
15 wrz 11:56
mcjng: ok i właśnie teraz cały problem pojawia się w tym, że nie wiem jak to narysować.
15 wrz 12:38
Mila: Co chcesz narysować?
15 wrz 14:40
mcjng: [f(x)+1]*[2−f(x)] ≥ 0 czyli parabola, ale nie wiem jak odwrocona
15 wrz 16:12
Basia:
[ f(x)≥−1 i f(x)<2 ] lub [ f(x)≤ −1 i f(x)> 2 ] ⇔
[ f(x)≥−1 i f(x)<2 ] lub fałsz ⇔
[ f(x)≥−1 i f(x)<2 ]
reszta zależy od f(x)
dla różnych funkcji to będzie bardzo różnie i wcale nie musi to być parabola
15 wrz 16:17
mcjng:
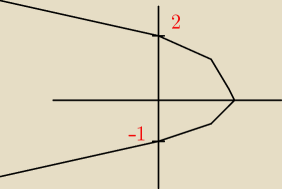
tak by to wyglądało?
15 wrz 16:23
Basia: co Ty rysujesz ?
| | f(x)+1 | |
przecież to jak będzie wyglądał wykres |
| |
| | 2−f(x) | |
zależy od tego jaką funkcją jest f(x)
| | 2x+1 | |
np. dla f(x) = 2x dostaniesz funkcję homograficzną y = |
| |
| | 2−2x | |
| | x2−1 | |
a dla f(x) = x2 coś zupełnie innego y = |
| |
| | 2−x2 | |
napisz no lepiej pełną treść zadania
od początku
15 wrz 16:35
Mila: Witaj Basiu, właśnie to samo pomyślałam− pełną treść zadania chciałabym znać.
15 wrz 18:54


 1) wykres:
|f(x)|=x2−4
|y|=x2−4
|y|=y dla y≥0⇔y=x2−4 (wykres tylko nad osią OX)
|y|=−y dla y<0
−y=x2−4
y=−x2+4 ( wykres tylko pod osią OX)
Nie umiem narysować − w każdym bądź razie odrzucasz wykresy dla x∊(−2;2) (te z wierzchołkami)
1) wykres:
|f(x)|=x2−4
|y|=x2−4
|y|=y dla y≥0⇔y=x2−4 (wykres tylko nad osią OX)
|y|=−y dla y<0
−y=x2−4
y=−x2+4 ( wykres tylko pod osią OX)
Nie umiem narysować − w każdym bądź razie odrzucasz wykresy dla x∊(−2;2) (te z wierzchołkami)
 tak by to wyglądało?
tak by to wyglądało?