Oblicz pole powierzchni całkowitej i objętość ostrosłupa Jula: Podstawą ostrosłupa ABCS jest trójkąt prostokątny o przyprostokątnych AC i BC długości 4cm. Krawędzie boczne tego ostrosłupa też mają długość 4 cm. Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa. Z góry dziękuję

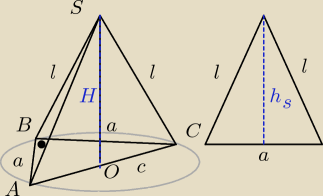
dero2005: AB = BC = a = 4 AS = BS = CS = l = 4 AC = c = a√2 = 4√2 OC = ^c₂ = 2√2 H = √l² − (^c₂)² = √4² − (2√2)² = √16 − 8 = √8 = 2√2 h_s = √l² − (^a₂)² = √4² − 2² = √16−4 = √12 = 2√3 P_p = a² = 4² = 16 → pole podstawy

	c*H		a*hs		4√2*2√2		4*2√3
Pb =		+ 2*		=		+ 2*		= 8 + 8√3 = 8(1+√3)
	2		2		2		2

P_c = P_p + P_b = 8(3+√3) V = ¹₃*P_p*H = ³²₃√2

dero2005: błąd!

	a2		42
Pp =		=		= 8
	2		2

P_c = 8(2+√3)

	16
V =		√2
	3

Jula: Dziękuję jak nie wiem co, życie mi uratowałeś