Romb AmD: łatwe zadanko: oblicz miary kątów rombu wiedząc że symetralna boku rombu zawiera jego wysokość

zuom: kwadracik?

ICSP: dwa po 60 oraz dwa po 120

ICSP: gdzie w kwadracie wysokość ?

AmD: dziekue. a jak do tego dojść? nie pojmuje

Eta:

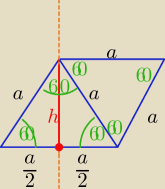
gość: Krótsza przekątna rombu dzieli go na dwa trójkąty równoboczne. W innych przypadkach masz trójkąty równoramienne, ale podstawa jest nie tam gdzie by się chciało.

gość: tzn podstawa tych trójkątów

ICSP: a − bok

1
	a − odcinki na jakie podzieliła wysokość bok na który pada.
2

α − kąt ostry rombu

	1
cosα =		⇒ α = 60o. Drugi zatem ma 120o koniec zadania
	2

Bogdan: Ja też ICSP jestem ciekaw, jak doszedłeś do podanych przez siebie wyników.

AmD: dziekuje uprzejmie

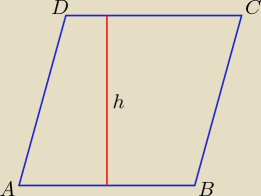
Bogdan: Ta symetralna boku AB też zawiera wysokość rombu

zuom: stąd mój tekst o kwadracie ale chyba w "zawiera" miało jednak chodzić o to, by linie te się pokrywały

Bogdan: Brak w zadaniu informacji, że symetralna boku przecina wierzchołek rombu.

Eta:

ICSP: widocznie treść jest niedopracowana Inaczej będzie istniało nieskończenie wiele rombów które będą spełniać warunki zadania

Bogdan: Nie można również przyjąć, że ten romb jest kwadratem, bo w treści zadania jest mowa o symetralnej boku, a nie boków. Każda symetralna boku rombu zawiera odcinek o długości równej wysokości rombu, czyli mówiąc skrótowo, zawiera wysokość rombu.

Eta:

Eta: Ta "przytulanka" .... dla ICSP

Bogdan: Każdy romb spełnia warunki zadania. Zadanie zawiera za mało danych, by można je rozwiązać.

AmD: tresc z podrecznika dla matematyki dla 2 liceum

AmD: i mam jeszcze jedno : oblicz szerokosc prostokatnej ramy obrazu wiedzac ze obwod zewnetrzny ramy jest o 28 cm wiekszy od obwodu wewnetrznego tej ramy

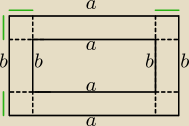
gość.: Obw(w) = 2(a+b) Obw(z) = 2(a+b) + 28 = 2(a+b+14) to 14 dzielimy na 4 (zielone krawędzie) i daje 3,5