, kasia: oblicz długość promienia okręgu opisanego na trójkącie równoramiennym o bokach długosci 10 , 10, 14 cm

loitzl9006:

	abc
Skorzystaj ze wzoru P=
	4R

gdzie P − pole trójkąta, R − promień okręgu opisanego na trójkącie, a,b,c − długości boków trójkąta Trzeba przekształcić wzór tak, aby wyznaczyć z niego szukane R. Potem policzyć pole trójkąta P i wstawić do wzoru. Gdyby było coś niezrozumiałego − pisz.

kasia: dzięki wyszło

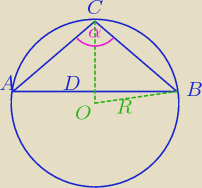dero2005: AB = 14 AC = CB = 10 sprawdzamy czy kąt α jest > 90^o AB² = BC*AC − 2AC*BC*cosα 14² = 10*10 − 2*10*10*cosα 196 = 100 − 200cosα cos α = − 0,48 α = 118,68^o > 90^o czyli tak jak na rys DC = √BC² − BD² = √10² − 7² = √51 CO = OB = R OD = R − DC = R − √51 z Pitagorasa R² = DB² + (R − √51)² R² = 7² + R² − 2R√51 + 51 R² = 49 + R² − 2R√51 + 51 2R√51 = 100 R√51 = 50

	50
R =		√51
	51