. kasia: oblicz sume odległości środka okręgu opisanego na trójkącie od jego boków o długościach 5 cm,

	7√3
7cm, 8 cm. Promień okręgu ma długosc		cm.
	3

Bogdan:

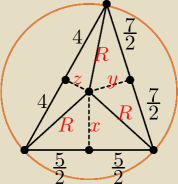
	7
R =		, przy czym ta liczba jest zbędną daną w zadaniu. Mając długości
	√3

boków trójkąta można obliczyć długość promienia okręgu opisanego na nim. Trzeba skorzystać z twierdzenia Pitagorasa i obliczyć wartości: x, y, z.

Eta: Witam Bogdanie Czy dobrze pamiętam? x+y+z= r+R

PW: Obliczmy odległość S (środka okręgu opisanego) od boku o długości 8. Jak wiadomo, S należy do symetralnej każdego z boków,, a więc rzut S na rozpatrywany bok leży pośrodku tego boku. Tworzy się trójkąt prostokątny, w którym przeciwprostokątną jest promień r okręgu opisanego, jedną z przyprostokątnych − połowa boku, a drugą przyprostokątną − szukana odległość p(zrób rysunek, to będzie to widać). Mamy więc p² + 4² = r²,

	7√3
p2 = (		}2 − 16
	3

	49
p2 =		−16
	3

	1
p2 =
	3

	1
p =
	√3

Następne odległości liczymy tak samo, licząc drugą odległość q weźmiesz połowę boku o długości 7, czyli 3,5 i licząc trzecią odległość s − połowę boku o długości 5, czyli 2,5. Żmudne, ale myślowo nietrudne. A teraz pytanie. Licząc cokolwiek powinniśmy sprawdzić, czy dane w zadaniu są spójne, krótko mówiąc czy nie wpuszczają nas w maliny. Jak sprawdzić, czy rzeczywiście trójkąt o bokach 5, 7, 8 jest wpisany w okrąg o podanym promieniu?

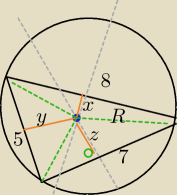
Mila: Sprawdzam jaki to Δ.(tw. cosinusów) 8²=5²+7²−2*5*7 cos∡C 64=25+49−70cos∡C 64=74−70cosC 10=70*cosC cosC>0 zatem Δ jest ostrokątny i środek okręgu opisanego na tym Δ leży wewnątrz trójkąta. Popielate linie to symetralne boków Δ

	7√3
z2+3,52=R2⇔z2+12,25=(		)2
	3

dokończ

PW: Pisaliśmy niemal jednocześnie z Bogdanem, a szkoda − powinna być jakaś sygnalizacja, że ktoś opracowuje temat. Nie dobijajcie Kasi, ona się dopiero uczy (ja też byłem okrutny).

Eta: za fatygę

Bogdan: Dobry wieczór Eta, Mila, PW x + y + z = R + r dla Ciebie Eto

	7√3		5*7*8
R =		, pole trójkąta P =		= 10√3
	3		7√3   4*   3

	1		10√3
p =		(5 + 7 + 8) = 10, pole trójkąta P = p*r ⇒ r =		= √3
	2		10

	7√3		10√3
x + y + z =		+ √3 =
	3		3

Można sprawdzić rodzaj trójkąta bez korzystania z twierdzenia cosinusów. a, b, c − długości boków trójkąta i a ≤ b ≤ c a² + b² > c² trójkąt ostrokątny, środek okręgu opisanego jest wewnątrz trójkąta. a² + b² = c² trójkąt prostokątny, środek okręgu opisanego jest w środku przeciwprostokątnej. a² + b² < c² trójkąt rozwartokątny, środek okręgu opisanego jest na zewnątrz trójkąta.

kasia: jeeeeej dziękuje bardzo

Eta: dla Bogdana

PW: Kasiu, nie załamuj się, oni tak specjalnie. Za chwilę wrzucą ten trójkąt w układ współrzędnych i scałkują funkcję sklejoną z dwóch funkcji liniowych, żeby obliczyć pole.

Bogdan: