wykre funkcji szklanka: jak naszkicować ten ↓wykres f(x)=x²+x+1 zaczynam od wierzchołka o będzie wynosił 0 potem robię tabelkę i nanoszę punkty tak?

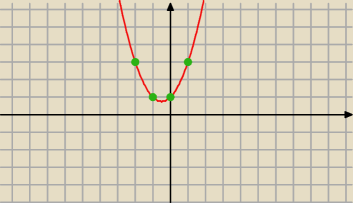
Aga1.: Wierzchołek W=(p,q) Gdzie

	−b		−1
p=		=
	2a		2

	1		−1		1
q=f(p)=f(−		=(		)2=		+1=
	2		2		2

Punkt przecięcia paraboli z osią Oy to (0,c)=(0,1)

szklanka: czyli jak mamy samo x to jest to ukryte 1 ,tak?

Aga1.: Tak, a jak −x to ukryte −1.

szklanka: chce sobie ten wykres przesunąć o wektor −1 i −3 Robię po prostu tak −1 o jeden w lewo −3 o trzy w dół Gdy robię natomiast podkładając pod f(x)=x²+x+1 czyli f(x)=(x+1)²+(x+1)+1−3 wychodzą zupełnie inne współrzędne wierzchołków gdy robię "ręcznie" a jeżeli podstawiając , o co chodzi?

szklanka: Natomiast gdy wykres pierwotny przekształcam w ten sposób f(−x) to robiąc "ręcznie" wychodzi mi tak samo jak bym robił podstawiając do wzoru . Nie wiem dlaczego tylko w przypadku z wektorami nie zgadzają się oby dwa sposoby.

szklanka: oba*

krystek: Tak nie wolno podstawiać !

szklanka: w książce jest wynik x²+3x jeżeli chodzi o przesunięcie o wektor −1 −3 , niby skąd ten wynik wyszedł x² +3x? Właśnie podstawiając f(x)=x²+x+1 czyli f(x)=(x+1)²+(x+1)+1−3

krystek: x'=x+(−1) y'=y+(−3) i teraz podstawiasz za x=x'+1 y'=y+3

Aga1.: (x+1)²+(x+1)+1−3=x²+2x+1+x+1+1−3=x²+3x

krystek: y=x²+x+1 po przesunięciu o wektor [−1;−3} mamy y'+3=(x'+1)²+(x'+1)+1 y'=x'+1)²+(x+1)+1−2 y'=x²+3x jest funkcja po przesunięciu o wektor danej funkcji.