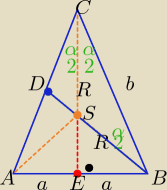
zadanie tn: Witam, W trójkącie równoramiennym ostrokątnym ABC mamy dane |AC | = |BC | = b oraz |∡ACB | = α . Z wierzchołka B przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok AC w punkcie D . Oblicz promień okręgu wpisanego w trójkąt ABC. Powiedz mi czy moje rozwiązanie też jest ok? Odpowiedź w zbiorze jest taka:

b sinα
2sin(α2)+1

Ja otrzymuję inną, nie wiem czy taka odpowiedź dostanie max punktów? co o tym sądzicie? Jak to byłoby ocenione na maturze, a czasem takie zadania się trafiają P.S przedstawiam nawet dwa sposoby

tn: aj, zapomniałem dodać linka, zaraz dam

tn: http://i.imgur.com/pzbzK.jpg

Bogdan: czy na pewno chodzi o promień okręgu wpisanego w trójkąt ABC, a może to ma być trójkąt ABD?

tn: nie, ABC

Eta:

	bsinα
Odp: r=
	α   2(sin +1)   2

tn: no tak, ale czy moje rozwiązanie jest ok ?

Eta:

a		α		α
	= sin		⇒ a=b*sin
b		2		2

	b2*sinα
P(ΔABC)=
	2

	2P		2P		P
rw=		=		=		=.... dokończ
	ob		2a+2b		a+b

tn: ok, ale co o moim rozwiązaniu ?

Eta: Czy treść zadania jest poprawna? Informacja o prostej BD jest tu zbędna do wyznaczenia r_w −− wpisanego w trójkąt ABC (dlatego pytam o treść ?

tn: Wiem, ale to możemy pominąć, w zadaniu jest też podpunkt b), A ja zastanawiam się nad a)