koło opisane na trójkącie Tynia: Błagam, może mi ktoś pomóc ? Jestem kompletnie zielona jeśli chodzi o to zadanie W trójkącie prostokątnym o obwodzie 9 długości boków tworzą ciąg arytmetyczny. Oblicz pole koła opisanego na tym trójkącie.

Maslanek: Mamy trójkąt prostokątny. Więc środek koła opisanego na trójkącie znajduje się na przeciwprostokątnej − dokładniej na jej środku. Mamy, że a+b+c=9 i z tw. Pitagorasa a²+b²=c². Dodatkowo z ciągów 2b=a+c.

Maslanek: Czyli b=3. Więc a+c=6 a²−c²=−9 a+c=6 (a−c)(a+c)=−9 6a−6c=−9 a+c=6 a=27/12 b=3 c=45/12 Wyniki do sprawdzenia.

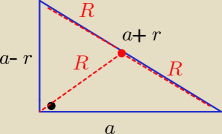
Eta: r−−− różnica ciągu arytmetycznego r €(0,a) a−r+a+a+r=9⇒ 3a=9 ⇒a=3

	3		3		15
(3−r)2+32=(3+r)2 ⇒ r=		to: c=2R= 3+		=
	4		4		4

	c
R=		=...
	2

P(k)= πR²=....