...
maturzystka:
Wysokość ostrosłupa prawidłowego trójkątnego tworzy z krawędzią boczną tego ostrosłupa kąt α
taki że cos α= 0,8. Krawędź podstawy ma długość 3. Oblicz pole powierzchni tego ostrosłupa.
PW: Niech trójkąt ABC będzie podstawą ostrosłupa, S jego wierzchołkiem, a OS wysokością. Z
definicji ostrosłupa prawidłowego wynika, że O jest punktem, w którym przecinają się
symetralne boków trójkąta ABC. Wiadomo, że jeśli a jest bokiem trójkąta równobocznego, to
co wynika z faktu, że symetralne boków są również wysokościami, a wysokości przecinają się w
| | 2 | |
|
| licząc od wierzchołka. |
| | 3 | |
| a√3 | |
| to wysokość trójkąta, tutaj a=3, więc po podstawieniu otrzymamy |
| 2 | |
|AO| =
√3.
W trójkącie prostokątnym AOS wiemy, że kąt OSA = α, cosα=0,8. Oznacza to, że
|OS| = |AS|cosα.
Z twierdzenia Pitagorasa
|OS|
2 + |AO|
2 = |AS|
2,
po podstawieniu danych
|AS|
20,8
2 +
√32 = |AS|
2,
Stąd już łatwo wyliczyć |AS|. Jeśli to mamy, trójkąt − ściana boczna − ma znane boki, a więc
można policzyć powierzchnię, choćby wzorem Herona. Rysunek, szczegóły obliczeń i za godzinę
można iść spać. Dobranoc.
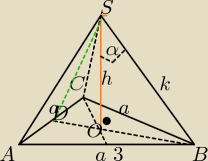 W ΔSOB:
W ΔSOB:
