rozwiąż nierówność : [ -1/2x + 1 ] ≤ 3 wojtek: rozwiąż nierówność : [ −1/2x + 1 ] ≤ 3

Piotr: a co to za nawias i po co on ?

Eta:

	1
Myślę,że ma być: |−		x+1|≤ 3
	2

wojtek: bo to całość jest

Piotr: Witam Eto jaka calosc wojtek ?

wojtek: symbol [a] oznacza największą liczbę całkowitą , nie większą niż a

Eta:

	1
|−		x+1|≤3 /*2
	2

|−x+2|≤6 ⇔ |−(x−2)|≤6 |x−2|≤6 x€ ...... dokończ

Piotr:

wojtek: nie chodiz mi o wartość bezwzględna tylko o całość : klasa 2 liceum

Eta: Myślałam,że to wartość bezwzględna

wojtek: no ok , ale jak tą nierówność zrobić ?

Timmy:

	1		1		1		1
[−		x + 1] ≤ 3 ⇔ [−		x] + 1 ≤ 3 ⇔ [−		x] ≤ 2 ⇔ −		x < 3 ⇔ x > −6
	2		2		2		2

wojtek: a dlaczego pod koniec wyniku sie zmienia znak z ≤ na < ?

Timmy: Masz coś takiego: [a] ≤ 2. Gdy a ∊ (−∞ ; 2> To nierówność jest oczywiście spełniona. Gdy a ∊ (2; 3) wtedy [a] = 2, więc też. Gdy a = 3, to [a] = 3, więc już nie. Gdy a ∊ (3; +∞), to [a] ≥3, też odpada.

Bogdan:

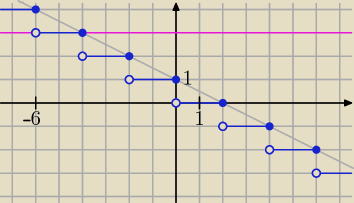
	1
To jest ilustracja nierówności: [−		x + 1] ≤ 3
	2

	1
y = [−		x + 1] (niebieski wykres)
	2

y = 3 (różowy wykres)

	1
Wykres y = [−		x + 1] pokrywa się z wykresem y = 3 lub leży poniżej tego wykresu
	2

dla x > −6