?? Mleko: W trapezie równoramiennym ABCD przekątna trapezu ma długość 13cm, a odcinek łączący srodki ramion ma dlugosc 12 cm. Oblicz pole czworokata powstalego przez polaczenie kolejnych srodkow bokow trapezu. Jaki to czworokat?

Mleko:

tim: Ok. Ja.

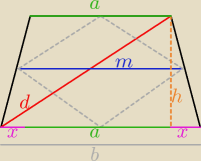
tim: Ok, więc tak. DANE: m = 12 d = 13

	a + b
m =		→ 2m = a + b → 24 = a + b
	2

b = a + 2x → 24 = 2a + 2x → 12 = a + x Korzystamy teraz z trójkąta prostokątnego d, a+x, h 12² + h² = 13² h = 5

	d1 * d2
Figura ta jest rombem więc P =		. Podstaw to co masz i proszę
	2

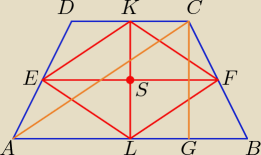
Bogdan: a − długość dolnej podstawy trapezu, b − długość górnej podstawy trapezu

	a + b
|EF| =		= 12
	2

|AC| = 13

	a + b
|AG| =		= 12
	2

|KL| = |CG| = √13² − 12² = 5

	1		1
Figura ELFK jest rombem, którego pole P =		*|EF|*|KL| =		*12*5 = 30
	2		2

Mleko: a co to jest d1 i d2?

tim: Eh

tim: Przekątne rombu

Bogdan: Teraz ja timie wlazłem Ci w paradę, ale nie widziałem jeszcze Ciebie, gdy zacząłem pisać rozwiązanie

Mleko: dobra juz wiem...

tim: Nie widziałeś Ok, ja?

tim: Zresztą nic nie szkodzi

Piotrek: jak udowodnic ze powstala figura to romb? czy wystarczy pokazac ze przekatne przecinaja sie pod katem prostym?

Piotrek: ktos pomoze?

Janek191: Stosujemy tw. Talesa.