nierówności wielomianowe Asia: Proszę Was o pomoc! Nie chcą mi wyjść 3 nierówności wielomianowe. a) 2x³ − 6x² + 8 ≤ 0 b) 2x⁴ + 3x³ < 11x² +6x c) −3x³ + 6x² + 5x ≤ 2x⁴ +6 Proszę Was o pomoc, to niezwykle ważne

ZKS: Jaki masz problem z podpunktem a)? Pierwiastka nie możesz znaleźć?

Asia: delty nie mogę tu wyliczyć, wiec jak?

asdf: na przykład grupowaniem

ZKS: A potrafisz liczyć Δ dla wielomianów stopnia trzeciego?

Asia: no nie, ostatni przykład wyliczyłam.. a jakbyście pogrupowali podpunkt a?

ZKS:

	1
2x3 − 6x2 + 8 ≤ 0 / *
	2

x³ − 3x² + 4 ≤ 0 x³ + x² − 4x² + 4 ≤ 0 Teraz grupuj.

ZKS: To zaprezentuj jak policzyłaś Δ w ostatnim i jak rozwiązałaś nierówność w ostatnim przykładzie.

asdf: 2x³ − 6x² + 8 =< 0 2x³ − 8x² + 2x² + 8 =< 0 2x²(x + 1) − 8(x² − 1) =< 0 dasz rade dalej ?

Asia: dużo pisania, ale ostatni przykład rozwiązałam tak, że sprawdzalam co pasuje pod ową nierówność, w sensie jaki pierwiastek, pasowało −2, także podzieliłam nierówność przez dwumian x+2 natomiast kolejną nierówność również sprawdziłam i pasowało −3/2 − otrzymałam równanie kwadratowe, z którego wyliczyłam delte i oto otrzymałam 3 pierwiastki − narysowalam wykres i otrzymałam rozwiązanie

Asia: dziękuję

ICSP: ZKS umiem liczyć deltę dla wielomianów stopnia III Miło że pytasz

ZKS: Wiem że Ty ICSP umiesz liczyć Δ dla wielomianów stopnia trzeciego myślałem że koleżanka też umie jednak tu się myliłem. Jednak chciałbym abyś zapisała jak to rozwiązywałaś.

ICSP: Czekaj Czy to mój drogi ZKS nie miałeś wczoraj rozłożyć na czynniki pewnego wielomianu ?

ZKS: Mnie wczoraj nawet chyba nie było na forum a co to za wielomian mam nadzieje że tylko nie Twojej roboty.

ICSP: nie to był : x⁴ + 10x³ + 90x + 81 z poleceniem rozłożenia na czynniki W końcu sam go rozłożyłem bo nikt nie chciał

asdf: To ja dokończę może to co umiem 2x²(x + 1) − 8(x² − 1) =< 0 x²(x + 1) − 4(x + 1)(x − 1) =< 0 (x + 1)(x² − 4x + 4) =< 0 (x + 1)(x − 2)² =< 0 x ∊ (−∞;−1>

ICSP: i źle

asdf: x ∊ (−∞; −1> oraz 2

ICSP:

asdf: Przy Tobie to się nauczę dokładnie patrzeć na zapisy

ICSP:

Asia: nauczcie mnie liczyć delte z wielomianów stopnia III

ICSP: lepiej będzie Ciebie nauczyć twierdzenia Bezouta i schematu Hornera. Δ dla wielomianów stopnia > 2 wygląda paskudnie + trzeba znać parę sztuczek aby w ogóle rozwiązać jakiś wielomian sposobem z deltą.

asdf: a jedna ze sztuczek to: zapytaj ICSP

Asia: znam twierdzenie Bezout oraz umiem Hornera.. jedynie mam pustke w głowie po dłuższym wolnym ale powoli wracam do wprawy

ICSP: no to nie powinnaś mieć problemów z rozkładem wielomianów Postaraj sie podszkolić grupowanie i już nie będzie problemu

Asia: generalnie nie mam bynajmniej z 17 przykładami / 20. Problem pojawia się gdy np 11x² muszę zamienić na różnice kwadratów albo coś dzięki jeszcze raz za pomoc

ICSP: a taki rozłożysz : x⁴ + 4 = Tylko nie pomagać Jak nie da rady to nie xD Może kiedyś się uda

ZKS: Może uda się go zrobić tylko że jest taki pogmatwany strasznie.

ICSP: Mówisz o x⁴ + 4

ZKS: Nie tym wyżej co podałeś. Bo mi coś ciągle się nie zgadzało ale wreszcie wyszło.

ICSP: łącznie trzy nawiasy powinny być

ZKS: Jeszcze sobie metodą Ferrariego sprawdziłem.

ICSP: Ona zawsze działa Tak z ciekawości spytam. W metodzie Ferrariego liczyłeś deltę czy od razu zauważyłeś że pasuje 9 ?

ZKS: Liczyć liczyłem ale można było od razu to zauważyć niestety jestem ślepy przez te wakacje.

ICSP: wystarczyło zauważyć że : 10y − 90 = 10(y−9) oraz y² − 81 = (y−9)(y+9)/ Wyciągnąć y = −9 przed nawias i koniec

ICSP: y−9 oczywiście

ZKS: Niestety jestem jeszcze ślepy.

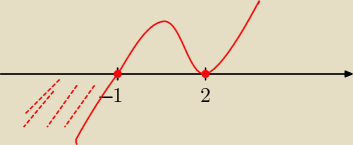
Gustlik: ad a) 2x³ − 6x² + 8 ≤ 0 /:2 x³ − 3x² + 4 ≤ 0 /:2 Schemat Hornera: "Kandydaci" na pierwiastek: +−1, +−2, +−4 1 −3 0 4 −1 1 −4 4 0 x=−1 jest pierwiastkiem (x+1)(x²−4x+4)≤0 (x+1)(x−2)²≤0 x=−1 v x=2 (2−krotny) Rysuje wykres, prawe ramię od góry, bo a>0. x∊(−∞, −1>U{2}

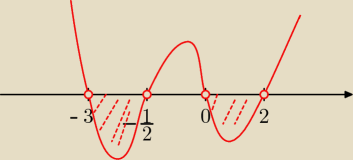
Gustlik: ad b) 2x⁴ + 3x³ < 11x² +6x 2x⁴ + 3x³ − 11x² −6x < 0 x(2x³ + 3x² − 11x −6) < 0 x=0 Wielomian z nawiasu rozkładam Hornerem: "Kandydaci" na pierwiastek:

	1		3
+−1, +−2, +−3, +−6, +−		, +−
	2		2

2 3 −11 −6 1 2 5 −6 −12 −1 2 1 −12 6 2 2 7 3 0 x=2 jest pierwiastkiem x(x−2)(2x²+7x+3)<0 Δ=25, √Δ=6

	1
x1=−3, x2=−
	2

	1
Pierwiastki: x=−3 v x=−		v x=0 v x=2
	2

a>0 więc prawe ramię do góry

	1
x∊(−3, −		)U(0, 2)
	2

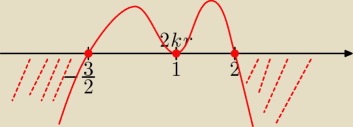
Gustlik: c) −3x³ + 6x² + 5x ≤ 2x⁴ +6 −3x³ + 6x² + 5x − 2x⁴ −6≤0 − 2x⁴−3x³ + 6x² + 5x −6≤0 Teraz Horner: "Kandydaci" na pierwiastki:

	1		3
+−1, +−2, +−3, +−6, +−		, +−
	2		2

−2 −3 6 5 −6 1 −2 −5 1 6 0 x=1 jest pierwiastkiem, mamy: (x−1)(−2x³−5x²+x+6)≤0 Jeszcze raz Horner: −2 −5 1 6 1 −2 −7 −6 0 x=1 jest pierwiastkiem drugi raz, a wiec 2−krotnym, mamy: (x−1)²(−2x²−7x−6)≤0 Δ=1, √Δ=1

	3
x1=−		, x2=2
	2

Mamy:

	3
x=1 (2−krotny) v x=−		v x=2
	2

a<o, więc prawe ramię w dół

	3
x∞, −		>U{1}U<2, +∞)
	2