Prostokąt wpisany w koło, stosunek dł. boków. michal1103: Prostokąt wpisany w koło ma pole π razy mniejsze od pola tego koła. Oblicz stosunek długości boków prostokąta.

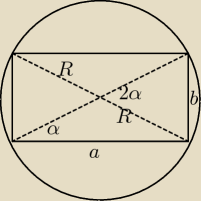
PW: Prostokąt ma zatem pole równe r², jeżeli r oznacza promień okręgu. Oznaczmy jeden z kątów między przekątnymi symbolem α, drugi z kątów między przekątnymi jest oczywiście równy π−α. Prostokąt jest sumą czterech trójkątów, które zgodnie ze znanym wzorem mają łączną powierzchnię

	1		1
2(		r2sinα +		r2sin(π−α)) = r2sinα + r2sin(π−α) = 2r2sinα.
	2		2

Tak więc z jednej strony pole prostokąta jest równe r², a przy liczeniu za pomocą kąta środkowego α jest równe 2r²sinα.: r² = 2r²sinα..

	1
Oznacza to, że 1 = 2sinα, sinα=		, czyli α = π/6 (α = 30°).
	2

Kąt między podstawą trójkąta a przekątną jest połową kąta α (twierdzenie o kącie środkowym i wpisanym opartym na tym samym łuku). Stosunek boków trójkąta jest równy

	α
sin		= sin 15°.
	2

Wartość tę można samemu policzyć z wzorów: sin²15°+cos²15°=1 i 2sin15°cos15°=sin30° rozwiązując ten układ równań. albo skorzystać z tablic, gdzie jest podana wartość sin15° (dokładna, nie przybliżenie dziesiętne). Wykonaj najpierw rysunek prostokąta wpisanego w koło − widać będzie dlaczego α jest kątem środkowym, a kąt między podstawą a przekątną − kątem wpisanym.

Ajaks: Zrobiłam innym sposobem, mam wartość dokładną, ale brzydki wynik. Jutro napiszę. Dobranoc.

PW: Ja się oczywiście pomyliłem bez rysunku, stosunek boków prostokąta to tgα, a nie sinα. Reszta dobrze, rozwiązując układ równań dostaniemy sin i cos, a wiec i tgα (jest on równy 2−√3, jeśli obliczamy stosunek krótszego boku do dłuższego). Mam za to jeszcze jeden sposób, strawniejszy dla tych, którzy funkcji trygonometrycznych nie lubią. Jeśli boki prostokąta mają długości a i b, to a²+b²=(2r)² ab=r i po podzieleniu stronami będzie

	a		b
		+		= 4
	b		a

	a
czyli szukany stosunek boków		=x znajdziemy rozwiązując równanie
	b

	1
x+		= 4,
	x

co będzie pewnie łatwiejsze. Pierwiastki będą dwa, ale nie zrażać sią − jeden to stosunek boku mniejszego do większego, a drugi odwrotnie.

MIla: ab=r² (literówka)

Eta: Ten drugi sposób jest ok

PW: Pewnie, że zgubiłem potęgę przy r o 23:58, ale widzę, że też nie śpicie (u mnie to ze starości).

MIla: I sposób ( jak u PW)

	a
P▭=ab, PO=πR2 szukane:
	b

Z warunków zadania : π*ab=πR² ⇔ab=R²

	1		1
P▭=4*(		R*R*sin(2α) )=R2⇔sin(2α)=
	2		2

2α=30 przy założeniu, że a<b α=15⁰

	b		a
tg150=		=2−√3 ⇒		=2+√3
	a		b

tg(15⁰)=tg(45⁰−30⁰) oblicz, albo odczytaj w tablicach wartość dokładną. II sposób: ( dość długi, często uczniowie tak robią) Z warunków zadania : π*ab=πR² ⇔ab=R² z tw. Pitagorasa: a²+b²=(2R)² a²+b²=4R² a²+b²=4ab⇔a²−2ab+b²=2R² (a−b)²=2R² dla a>b a−b=√2R a=b+√2R a*b=R²⇔b(b+√2R)=R² i b>0 b²+√2Rb−R²=0 Δ=6R² √Δ=√6R

	−√2R−√6R
b1=		<0 nie odpowiada warunkom zadania
	2

	−√2R+√6R
b2=
	2

	−√2R+√6R		√6+√2
a=		+√2R=		R
	2		2

a		√6+√2
	=		=2+√3
b		√6−√2