Nie wiem jak się za to zabrać:/ Kompletnie nie rozumiem tego:(
Kuba: Wyznacz (nie podaj) równania, w prostych w których zawierają się dwusieczne kątów jaki tworzą
proste o równaniach: y=2x i y=1/2x
11 wrz 16:46
Gong: masz dwie proste
y=2x
i
y=1/2x
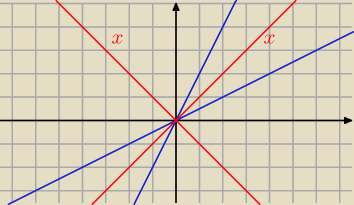
Jeśli narysujesz je sobie na wykresie, tworzą kąt. Dwusieczną będzie funkcja która jest hmm
jakby to ująć "pośrodku pomiędzy 1/2 a 2". Czyli:
2+1/2 = 5/2
5/2 : 2 = 5/4
y= 5/4x
chyba dobrze
11 wrz 16:55
Kuba: Jesteś pewny swojego wyniku?
11 wrz 17:04
Kuba: ?
11 wrz 17:23
Mila: Dwusieczna jest zbiorem punktów jednakowo odległych od ramion kąta.
Niech punkt P (x
0,y
0) należy do dwusiecznej kątów ,jaki tworzą dane proste ( będą dwa
rozwiązania)
m: 2x−y=0
d(P;m)=d(P;n) rozwiąż ten warunek
11 wrz 17:38
Kuba: Czy tak jest?
y=0<=>1/2x+0?
11 wrz 17:43
Kuba: m:2x=y
n: y=0<=>1/2x=0
Czy tak wygląda rozwiązanie?
11 wrz 17:50
Kuba: Mila?
11 wrz 17:55
Mila: Kuba, źle. Napisz warunek, który Ci podałam, umiesz?
11 wrz 17:55
Kuba: Nie, nie umiem:(
11 wrz 17:59
pigor: ... ,
czyli np. tak : niech (x,y) − dowolny (bieżący) punkt spełniający
równanie dwusiecznej, to jest on równoodległy od danych prostych , czyli
| |2x−y| | | |x−2y| | |
| = |
| ⇔ |2x−y| = |x−2y| /2 obustronnie (można, bo ?) ⇔ |
| √4+1 | | √1+4 | |
⇔ |2x−y|
2 = |x−2y|
2 ⇔ (2x−y)
2 = (x−2y)
2 ⇔ 4x
2−4xy+y
2 = x
2−4xy+4y
2 ⇔
⇒ 3x
2−3y
2= 0 ⇔ x
2−y
2= 0 ⇔ (x−y)(x+y)= 0 ⇔
⇔
x−y=0 ∨
x+y=0 − szukane równania dwusiecznych w postaci ogólnej , czyli
⇔
y=x ∨
y=−x − te same dwusieczne o równaniach w postaci kierunkowej . ...
11 wrz 17:59
Mila:
| |2x0−y0| | | |x0−2y0| | |
| = |
| |
| √22+12 | | √11+22 | |
||2x
0−y
0|=|x
0−2y
0|
można opuścić znaczki
2x−y=x−2y lub 2x−y=−x+2y
y=−x lub y=x
ilustracja
11 wrz 18:05
Kuba: Matko... Ale tego jest.... Dużo, ale rozumiem, że to jest już rozwiązane?
11 wrz 18:08
Mila: Tam na wykresie powinno być y=x i y=−x, coś mi zniknęło.(dwusieczne czerwone)
11 wrz 18:09
Kuba: Mila! Dziękuję! Tylko powiedz mi jeszcze skąd wziąłeś to 12 i 22 w mianowniku.
11 wrz 18:12
Mila: Jeżeli masz równanie ogólne prostej:
Ax+By+C=0 to wzór na odległość (x
0;y
0) od tej prostej jest taki:
W której jesteś klasie? To powinno być na lekcjach.
11 wrz 18:28
Kuba: Jestem w II LO
11 wrz 18:39
Mila: No, to będzie. Powodzenia.
11 wrz 18:45
Kuba: Jesteś już po maturze?
11 wrz 18:46
Mila: Uczę i pomagam na forum.
11 wrz 18:47