mat nat: w okrąg o promieniu 5 wpisano trójkat prostokątny .oblicz pole P tego trójkąta gdy cosinus jednego z kątów ostrych jest równy 1/3 .wynik zaokrąglij do jednego miejsca po przecinku

nat: jak to zrobić?

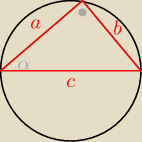
Ingham: R = 5 widać z rysunku, że: c = 2R = 10 teraz w trójkącie prostokątnym

	a		1
cosα =		=
	c		3

3a = c 3a = 10

	10
a =
	3

obliczamy z tw. Pitagorasa długość boku b (potrzebna do wzoru na pole, można też innym sposobem np. obliczyć z jedynki trygonometrycznej sinα) a² + b² = c²

	10
(		)2 + b2 = 102
	3

100
	+ b2 = 100
9

	100		900		100		800
b2 = 100 −		=		−		=
	9		9		9		9

	√800		20√2
b =		=
	3		3

	1		1		10		20√2		100√2
P =		ab =		*		*		=
	2		2		3		3		3

Ingham: pomyłka przy samym końcu:

	100√2
P =
	9

kaka: nie zgadza sie odpowiedz ma byc5,3 a nie 15,7