Całka oznaczona
Grzesiu: Dlaczego czasami w całce oznaczonej wyniki wychodzą ujemne przecież to jest pole obszaru prawda
?
11 wrz 13:47
Grzesiu: Pytam bo mam zadanie podobne do wczesniejszego a tam wartosci byly ujemne:
Funkcja f jest nieparzysta i continues(Ciągła ?) w R. Jeżeli ∫
5−2f(x)dx = 12, to
∫
52f(x)dx =

Możecie mi pomóc ? Co w ogóle oznacza to 12? To jest pole tej funkcji ?
11 wrz 14:01
Artur_z_miasta_Neptuna:
jeżeli liczysz pole powierzchni jakiegoś obszaru który jest PONIŻEJ osi OX (lub większość tegoż
obszaru) to całka wyjdzie Ci ujemna
policz sobie ∫−π/20 sinx dx
11 wrz 14:02
Artur_z_miasta_Neptuna:
skoro jest nieparzysta to:
∫−aa f(x) dx = 0
dla przykladu ∫−π/2π/2 sinx dx = 0
11 wrz 14:03
Grzesiu: a np jak mam funkcje x3 to jak ona jest ograniczona np z dołu to jest ten malutki kawałeczek
czy w dół do nieskończoności
11 wrz 14:07
Artur_z_miasta_Neptuna:
przeczytaj jeszcze raz to co napisałeś, bo ja niestety nie rozumiem o co Ci chodzi
11 wrz 14:11
Grzesiu: hmm to moze pomoglbys mi rozwiazac to zadanie ktore podalem albo chociaz odpowiedz dac co ?

11 wrz 14:13
Artur_z_miasta_Neptuna:
patrz mój wpis o 14:03 ... wniosek z niego wystarczy do napisania odpowiedzi.
11 wrz 14:21
Artur_z_miasta_Neptuna:
a '12' oznacza pole obszaru ograniczonego osią OX i funkcją f(x)
11 wrz 14:22
Mila:
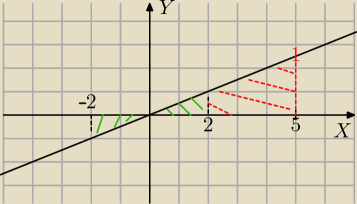 −2
−2∫
2f(x)dx=0
11 wrz 15:21
Grzesiu: Dziękuje mila za rysunek niestety jestem za ciasny żeby bez tego zrozumieć. Pozdrawiam

11 wrz 18:06
Mila: No, to jaki wynik?
11 wrz 18:07
Grzesiu : 12 ?
11 wrz 18:09
Mila: 
11 wrz 18:10
Grzesiu : Tylko ze ja to troszke inaczej zrobiłem oznaczyłem sobie od −2 do 0 jako y a od 0 do 2 −y, od
−2 do 5 12, a od 2 do 5 x. Więc wyszło równanie

12 = y−y+x
Wiem że z tego rysunku to odrazu widać ale niestety ja takiego ladnego nie narysowalem

Funkcja y = x jest nieparzysta ?

11 wrz 18:12
Mila: Wykres funkcji nieparzystej jest symetryczny względem punktu (0,0).
11 wrz 18:43
 Możecie mi pomóc ? Co w ogóle oznacza to 12? To jest pole tej funkcji ?
Możecie mi pomóc ? Co w ogóle oznacza to 12? To jest pole tej funkcji ?

 −2∫2f(x)dx=0
−2∫2f(x)dx=0


 12 = y−y+x
Wiem że z tego rysunku to odrazu widać ale niestety ja takiego ladnego nie narysowalem
12 = y−y+x
Wiem że z tego rysunku to odrazu widać ale niestety ja takiego ladnego nie narysowalem  Funkcja y = x jest nieparzysta ?
Funkcja y = x jest nieparzysta ? 