. :( Letty : wyznacz dziedzinę: 1.) log₂(x² + y) ≤ 1 2.) log_¹4(x² + y²) ≥ −1

Artur_z_miasta_Neptuna: kiedy log₂x ≤1 pamiętaj, że x>0

Letty : log₂x ≤ log₂2 ⇒ x ≤ 2

Letty : dalej nie wiem jaka jest dziedzina.

Artur_z_miasta_Neptuna: 0 < x²+y ≤ 2 czyli: 0 < x²+y ⋀ x²+y ≤ 2 −y < x² ⋀ y ≤ 2−x² y > x² ⋀ y ≤ −(x² − 2) rysujesz obie parabolki i zaznaczasz przedziały ... część wspólna = dziedzina

Letty : a dlaczego jeszcze x² + y musi byc większy od 0 ?

Artur_z_miasta_Neptuna: a czy wartość w logarytmie nie ma takiego warunku a widziałeś/−aś kiedyś log₂ (−1)

Letty : aha, no tak! ale głupie pytanie

Artur_z_miasta_Neptuna: zdarza się najlepszym

Letty : kurcze bo mi cos nie wychodzi..

Letty : x² + y > 0 ⇒ y > x² tak? czy y > −x²

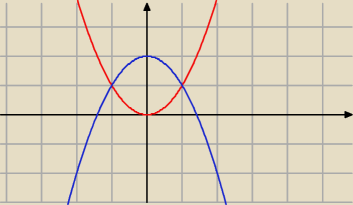
Artur_z_miasta_Neptuna: i masz obszar pomiędzy (bez czerwonej ... a z niebieską)

Artur_z_miasta_Neptuna: x²+y > 0 ⇔ x² > −y ⇔ y < −x²

Artur_z_miasta_Neptuna: źle narysowałem

Letty : ok, teraz juz wszystko jasne dzieki. ale mam jeszcze pytanie do tego drugiego przykładu. x² + y² > 0 ⇔ y² > −x² tak? i co dalej z ta dziedziną ?

Artur_z_miasta_Neptuna: x² +y² >0 to mój drogi (moja droga) jest nic innego jak cała płaszczyzna (R²) poza punktem (0,0) w końcu x²+y²>r² co oznacza ;> co to za obszar albo prościej x²+y²≤r²

Letty : nie rozumiem, dlaczego bez tego punktu (0,0) ?

Artur_z_miasta_Neptuna: a kiedy x²+y² ≤ 0 wtedy i tylko wtedy gdy x² = 0 oraz y² = 0 ... czyli bez punktu (0,0)

Letty : ok, czyli jak będe chciała to wszystko zaznaczyc na wykresie to poprostu wyjdzie mi takie koło o promieniu r = 2 bez punktu (0,0) tak?

Artur_z_miasta_Neptuna: si seniorita