Dzielenie płaszczyzny przez proste SuperM4n: "Na ile obszarów mogą podzielić płaszczyznę 3 różne proste? Rozważ różne przypadki." Nie za bardzo wiem, jak mam się zabrać do tego zadania i jak pokazać, na ile obszarów można podzielić płaszczyznę. Znaczy co? Narysować to jakoś? Czy może jakiś wzór jest? Nie mam pojęcia, proszę o pomoc.

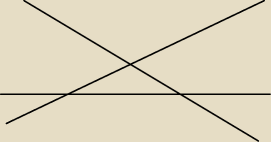
Mateusz: Wystarczy narysowac sobie to ale wczesniej zakładając ze proste mają sie przecinac czyli nie są równoległe i zadne nie beda przecinały sie w jednym punkcie i tak mamy ze jdna prosta dzieli płaszczyzne na dwa obszary 2 proste na 4 itd mozna wyznaczyc wzor ktory wyraza na ile obszarów n prostych moze podzielic płaszczyzne mozna zapisac wzor ciagu rekurencyjnego: {P₀=1 {P_n+1=P_n+n mozna wyznaczyc prosty wzor rozwiązując powyzsze równanie rekurencyjne rozwijając je i

	n(n+1)
otrzymując		więc proponuje ci najpierw odczytać sobie to z rysunku i potem
	2

sprawdzic za pomocą wzoru w ramach cwiczenia

Mateusz: Poprawka warunku "i zadne nie beda przecinały sie w jednym punkcie " powinno być: "i zadne 3 nie beda przecinały sie w jednym punkcie" po prostu nie dopisałem trojki